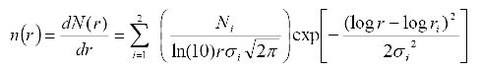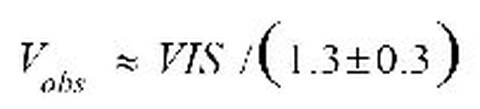Absolute Korrekturmodelle
Korrektur mithilfe MODTRAN
MODTRAN ist ein sehr gebräuchlicher Algorithmus. Er wird z.B. zur Korrektur von ASTER-Daten (Advanced Spaceborn Thermal Emission and Reflection Radiometer) verwendet. Programme, wie ATCOR, greifen ebenfalls darauf zurück.
Die Version MODTRAN 5 berechnet die atmosphärische Transmission, die atmosphärische Hintergrundstrahlung, einfach gestreute Sonnen- und Mondstrahlung, die direkte Bestrahlungssärke von Sonne und Mond sowie mehrfach gestreute Sonnen- und Thermalstrahlung.
Die spektrale Auflösung von MODTRAN beträgt v = 0,1 cm-1 FWHM (full-width half maximum) mit v... Wellenzahl (reziproker Wert der Wellenlänge).
Berücksichtigt werden die Absorptions- und Streueffekte von Molekülen sowie von Aerosolen. Zudem können auch vom Nutzer selbst gemessene Parameter mit in die Berechnungen einbezogen werden.
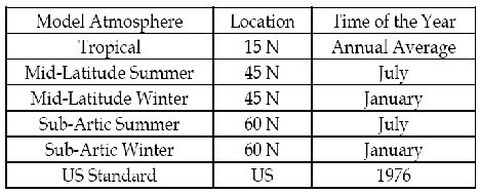
Vom Programm werden 6 verschiedene Atmosphärenmodelle zur Verfügung gestellt, die jeweils andere Parameter für
Temperatur
Druck
Dichte
Mischverhältnis von H20, O3, CH4, CO und N2O
als Funktion der Höhe enthalten, so dass die klimatischen Bedingungen möglichst gut angepasst werden können.
Der CO2 Gehalt kann vom Nutzer selbst eingegeben werden.
Die 6 verschiedenen Atmosphärenmodelle für die nördliche Halbkugel:
Die Korrekturmodelle beziehen sich auf Gebiete, die für einen hohen
Aerosolgehalt typisch sind:
ländliche Umgebungen, Städte, Wüsten und maritime Gebiete.
Zur Übertragung des Modells in die verschiedenen Atmosphärenschichten unterscheidet man die Bereiche:
0... 2 km: Erdoberfläche
2... 10 km: Troposphäre
10... 30 km: untere Stratosphäre
30... 100 km: obere Stratosphäre
Die 2 Schlüsselfunktionen der Modellierung des Aerosolgehalts:
genaue Repräsentation der chemischen und physikalischen Eigenschaften der Aerosolpartikel und die sich daraus ergebenden optischen Eigenschaften, wie z. B. der Brechungsindex
genaue Repräsentation der vertikalen Verteilung der Aerosolpartikel, also die Konzentration in der Atmosphäre
Wie bereits erwähnt, werden ländliche, maritime, Wüsten- und Stadtgebiete unterschiedlich modelliert. Sie unterscheiden sich hauptsächlich in den Mischverhältnissen der einzelnen Moleküle.
Um die Verteilung der Teilchengrößen mathematisch darzustellen, wird die Summe aus zwei Verteilungsfunktionen gebildet (nach Shettle und Fenn):
mit: N(r) ... Dichte als Anzahl der Partikel mit Radius r
σ ... Standardabweichung
ri ... maximaler Radius
Ni ... Dichte als Anzahl der Partikel mit maximalem Radius
Aufgrund dieser Verteilung gelang es Shettle und Fenn die wichtigen Parameter in Tabellen aufzulisten.
Sie enthalten die Refraktionsindizes entsprechender Wellenlängen, die Anzahl und das Volumen der Verteilungen für jedes der 4 unterschiedlichen Gebiete.
Die Veränderung der Aerosol-Konzentration hängt von der Sichtbarkeit ab. Hierbei unterscheidet man zwischen der Sichtweite, die ein Beobachter wahrnimmt (V obs) und der meteorologischen Sichtweite VIS:
Davon ausgehend kann auch die Abhängigkeit des Aerosol-Extinktionskoeffizienten von der Höhe abgeleitet werden. Bei diesigen Wetterverhältnissen (VIS = 2... 10 km ) ist der Extinktionskoeffizient bis zu einer Höhe von 1km konstant. Bei klarer Sicht (VIS = 23... 50 km ) steigt der Extinktionskoeffizient exponentiell mit zunehmender Höhe.