Ther­moelektrische Ströme in laserinduzier­ten Schmelzbädern

Einleitung
Eine Möglichkeit, um beim Laserstrahlschweißen höhere Schweißgeschwindigkeiten und bessere Nahtqualitäten zu erzielen, ist der Einsatz externer statischer Magnetfelder in der Werkstückebene. Bei entsprechenden Schweißuntersuchungen an Feinkornbaustählen und Aluminiumlegierungen [1,2] konnte der Schmelzbadauswurf unterdrückt, die Oberraupenqualität verbessert und die Form der Nahtquerschnitte erheblich beeinflusst werden. Diese Phänomene sind aber von der Orientierung des Magnetfeldes zur Vorschubrichtung abhängig. Zur Erklärung dieser Richtungsabhängigkeit wurde die Existenz von thermoelektrischen Strömen im Schmelzbad postuliert [1,2]. Durch Wechselwirkung dieser Ströme mit dem externen Magnetfeld werden Lorentzkräfte im Schmelzbad generiert, die als Ursache für die  beobachteten Phänomene angesehen werden.
Ziel der Forschungsarbeiten ist, die Ursachen für thermoelektrische Ströme beim Laserstrahlschweißen aufzuzeigen, die Verteilung der thermoelektrischen Strom-dichte für verschiedene Materialien zu bestimmen und die theoretischen Daten mit den experimentellen Ergebnissen zu vergleichen.

Analyse
Thermoelektrische Ströme werden durch den Seebeck-Effekt hervorgerufen. Dieser besagt, dass in einem geschlossen Stromkreis aus zwei verschiedenen, homogenen und isotropen Metallen (A und B) eine Spannung induziert wird, wenn die zwei Kontaktpunkte unterschiedliche Temperaturen (T1 und T2) aufweisen. Die so induzierte Spannung ist durch

    U = (αA - αB) ( T1 - T2)          (1)

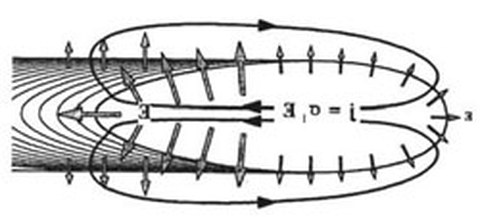
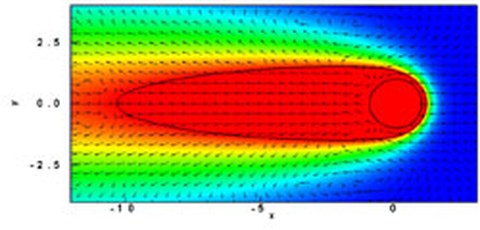
gegeben, wobei die Seebeck-Koeffizienten αA und αB temperaturabhängig sind und in der Größenordnung von 10-6 V/K liegen. In [1,2] wurde nun argumentiert, dass sich eine thermoelektrische Spannung zwischen dem Grundwerkstoff und der erstarrten Schweißnaht ausbildet, die eine homogene und gerichtete thermoelektrische Stromdichteverteilung im Schmelzbad nach sich zieht, siehe Abb. 7 in [1].
Die Berechnung der thermoelektrischen Stromdichte j startet mit der Onsager-Relation

      j = (σ/e) grad μ  -  α σ grad T        (2)

die die Stromdichte j linear mit Kräften gradμ und gradT verknüpft. Neben dem Seebeck-Koeffizienten α sind auch die elektrische Leitfähigkeit σ und das chemische Potential μ temperaturabhängig; e bezeichnet die elektrische Elementarladung. Mit der Beschränkung auf eine temperaturunabhängige Leitfähigkeit, eine zweidimensionale Geometrie und unter Nutzung von j=rot H sowie von div H=0 ergibt sich die Poisson-Gleichung

    (1/σ) ΔHz = (∂α/∂x) (∂T/∂y) - (∂α/∂y) (∂T/∂x)       (3)

Diese Differentialgleichung kann zusammen mit der entsprechenden Randbedingung für Hz analytisch gelöst werden [3], woraus sich die Komponenten von j mittels jx=∂Hz/∂y bzw. jy=-∂H/∂x ergeben.

Schlussfolgerung
Für Eisen konnte bei einer Peclet-Zahl von 4 (Die Peclet-Zahl ist ein Maß für das Verhältnis von konvektivem zu konduktivem Wärmetransport.) qualitativ die in [1,2] postulierte Stromdichteverteilung reproduziert werden. Damit lassen sich qualitativ die experimentell beobachteten Veränderungen in der Oberraupengestalt erklären. Für Aluminium wurden bei einer Peclet-Zahl von 1 Stromstärken ermittelt, die mit Werten zwischen 3 und 11 A im Bereich der experimentellen Werte von 8 bis 14 A liegen.

Literatur:
[1] M. Kern, P. Berger, and H. Hügel, Schweißen & Schneiden, 52, 140, 2000
[2] M. Kern, P. Berger, and H. Hügel, Welding Journal, 79, 72s, 2000
[3] J. Paulini, G. Simon, and I. Decker, J. Phys. D, 23, 486, 1990

Kontakt:
Dipl.Ing. Frank Brückner
Tel.: +49 (0) 351 83391 3452