Numerische Simulationsmethoden
Numerische Simulationsmethoden kommen in zahlreichen Bereichen von Forschung und Entwicklung zum Einsatz. Zur Auslegung komplexer neuartiger Materialien und innovativer Leichtbaustrukturen ist zunehmend eine integrative Prozess-, Material- und Bauteilmodellierung erforderlich. Diese stellt hohe Anforderungen an die Genauigkeit und Effizienz der Verfahren und erfordert zudem eine Verbesserung der Interaktion von Design und Auslegung, d.h. die Integration von CAD und CAE.
Um mittels numerischer Simulationsmethoden zum Verständnis komplexer Prozess-Struktur-Eigenschafts-Beziehungen beitragen zu können, müssen u.A. die lokale Werkstoffstruktur und deren Evolution modelliert werden. Ein Schwerpunkt der Professur für Numerische und Experimentelle Festkörpermechanik liegt daher in der Modellierung starker und schwacher Diskontinuitäten, die beispielsweise bei der Modellierung von Risswachstum, bei Entmischungsvorgängen oder in heterogenen Materialien vorkommen. Die abzubildenden Grenzflächen können dabei mittels eines diskreten oder eines diffusen Grenzflächenmodells beschrieben werden. Im diskreten Grenzflächenmodell wird die Grenzfläche explizit beispielsweise durch Elementkanten repräsentiert. In einem diffusen Grenzflächenmodell wird die scharfe Grenzfläche hingegen verschmiert und im Rahmen eines Phasenfeldmodells implizit mittels eines Ordnungsparameterfeldes beschrieben.
Um die genannten Grenzflächenmodelle weiterentwickeln und effizient anwenden zu können, arbeitet die Professur für Numerische und Experimentelle Festkörpermechanik an der Entwicklung verschiedener nicht konventioneller Diskretisierungsverfahren. Für die numerische Modellierung diskreter Grenzflächenbeschreibungen kommt die erweiterte Finite-Elemente-Methode XFEM zum Einsatz. Die aus der Phasenfeldmodellierung resultierenden partiellen Differentialgleichungen höherer Ordnung und starke lokale Gradienten des Ordnungsparameterfeldes werden durch adaptive isogeometrische Diskretisierungen abgebildet:
IGA

Isogeometrische Diskretisierung: Bézierkurve mit Kontrollpunkten
Die Isogeometrische Analyse (IGA) wurde entwickelt um die Konvertierung von CAD- in entsprechende FEM-Modelle zu erleichtern. Dafür werden zur Approximation der Feldvariablen im numerischen Modell dieselben B-Spline Basisfunktionen verwendet, welche auch zur Darstellung der Geometrie im CAD-Modell genutzt werden. Dadurch wird einerseits der geometrische Diskretisierungsfehler eliminiert. Andererseits bildet bereits das gröbste Berechnungsnetz die Geometrie exakt ab. Daher bietet die IGA ein ideales Diskretisierungsverfahren zur Anwendung adaptiver lokaler Netzverfeinerungstechniken. Weiterhin bietet die höhere Stetigkeit der B-spline Basisfunktionen über Elementgrenzen hinweg einen direkten Zugang zur numerischen Lösung von Differentialgleichungen höherer Ordnung. Die IGA stellt damit ein perfektes Werkzeug zur Berechnung diffuser Grenzflächenmodelle dar.
X-FEM
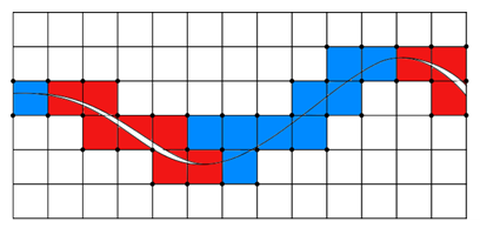
XFEM-Modellierung von Materialgrenzen und GrenzflächenrissenErweiterte Finite Elemente Methode (XFEM)
Ursprünglich für Rissfortschritts-simulationen entwickelt, kann die Erweiterte Finite-Elemente-Methode (XFEM) auch zur Abbildung von Einschlüssen, Hohlräumen oder Materialgrenzen verwendet werden. Im Unterschied zur gewöhnlichen FEM, bei der die Vernetzung an Details der zu simulierenden Struktur angepasst werden muss, ist dies bei Nutzung der XFEM nicht erforderlich. Risse und innere Grenzflächen, die bei Hohlräumen, Einschlüssen oder Materialgrenzen auftreten, sind nicht Teil des regelmäßigen Netzes. Die Lage der Unstetigkeitsstellen wird netzunabhängig durch eine lokale Anreicherung des gewöhnlichen Verschiebungsansatzes der FEM in einem regelmäßigen Berechnungsnetz abgebildet. Die XFEM ist damit in der Lage, Grenzflächen bei geringem Vernetzungsaufwand diskret abzubilden.
Adaptive Verfahren
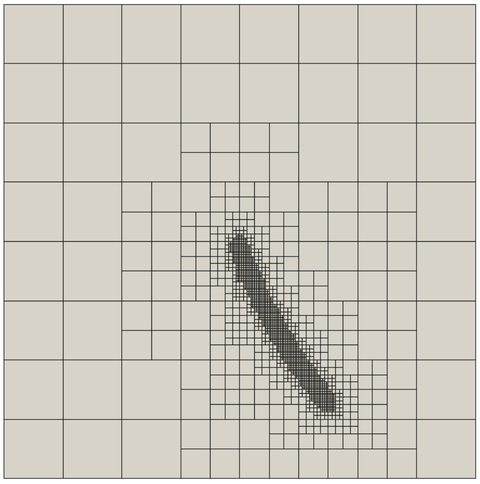
Adaptive Isogeometrische Modellierung des Rissfortschritts
Die Modellierung des Materialverhaltens an Grenzflächen in inelastischen Materialien ist mit dem Auftreten von starken örtlichen und zeitlichen Gradienten der Feldgrößen verbunden. Für die hinreichend genau Approximation und die effiziente Simulation dieser Probleme werden Algorithmen zur lokal und zeitlich adaptiven Verfeinerung bzw. Vergröberung des Berechnungsnetzes benötigt. Zur Anwendung dieser adaptiven Verfahren müssen Fehlerschätzer entwickelt und daraus Verfeinerungs- bzw. Vergröberungsbedingungen abgeleitet werden. Ein weiterer Forschungs-schwerpunkt ist die Untersuchung adaptiver Verfahren in Bezug auf Stabilität und Konvergenz.
Die Ergebnisse dieser Forschungsschwerpunkte fließen direkt in die Ausbildung Studierender der Vertiefungsrichtung "Simulationsmethoden des Maschinenbaus" ein.
