Non-adiabatic Quantum Molecular Dynamics
Table of contents
Introduction
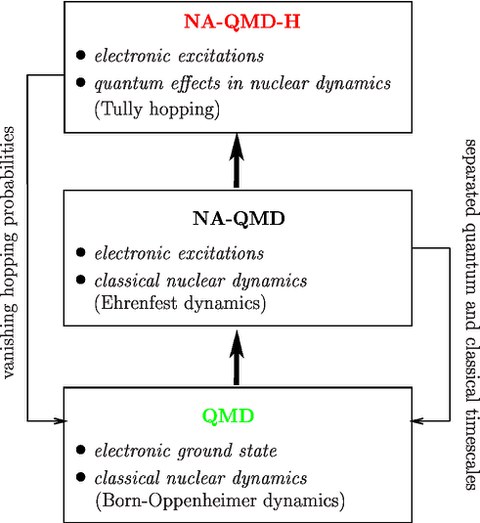
Hierarchy of ab initio MD methods: QMD, NA-QMD and NA-QMD-H. The left and right linkages indicate that both non-adiabatic approaches naturally merge into the adiabatic QMD limit under certain conditions.
The Non-adiabatic Quantum Molecular Dynamics (NA-QMD) is an ab initio method to describe the combined dynamics of excited electrons and nuclei in finite atomic many-body systems. This method has been developed, permanently extended and applied by us during the last years.
The approach is based on classical molecular dynamics for the nuclei self-consistently coupled with time-dependent density functional theory (TDDFT) for the electrons. When electronic excitations are switched off, the NA-QMD formalism reduces to its adiabatic limit
called Quantum Molecular Dynamics (QMD).
Recently, the NA-QMD theory has been considerably extended to include also quantum effects in the nuclear motion by combining the formalism with trajectory surface hopping: NA-QMD with hopping (NA-QMD-H).
Numerics
The numerical implementation of QMD, NA-QMD and NA-QMD-H is based on a basis expansion of the electronic Kohn-Sham functions and allows the simultaneous description of all electrons, e.g. strongly bound core electrons, weakly bound valence electrons and free electrons. Another advantage of the basis expansion
is the freedom to trade accuracy against computational effort by using different basis sizes. Currently available exchange-correlation functionals are the exact Hartree-Fock exchange, L(S)DA, LDA, and (for the electronic groundstate) LDA with self interaction correction. QMD, NA-QMD and NA-QMD-H allow to study the structure and dynamics of atomic, molecular and cluster systems in a wide range of scenarios.
Scenarios
|
Structure properties |
Dynamics in laser fields |
Dynamics in collisions |
|---|---|---|
|
|
|
Dynamics in laser fields
Dynamics in collisions
Publications
Theory: see here
Applications: see here
People
The formalism has been mainly developed by
-
Prof. Dr. Rüdiger Schmidt (group leader)
-
Prof. Dr. Ulf Saalmann
-
Dr. Olaf Knospe
-
Dr. Thomas Kunert
-
Dr. Mathias Uhlmann
-
Dr. Michael Fischer
Collaboration with experimental groups of
-
Prof. Dr. M. Barat (Université Paris-Sud)
-
Prof. Dr. E.E.B. Campbell (University Edinburgh)
-
Prof. Dr. I .V. Hertel (MBI Berlin)
-
Prof. Dr. H. O. Lutz (Universität Bielefeld)