Markus Löschner

Einfluss der Kontaktbeschreibung in FE-Modellen auf das Last-Verformungsverhalten von statisch und zyklisch beanspruchten Bauteilen

Einleitung

Für bestimmte Geotechnische Probleme, die mit der Methode der finiten Elemente berechnet werden, beispielsweise ein Pfahl, ist die Modellierung des Boden-Bauteil-Kontakts von immenser Bedeutung, da Ungenauigkeiten zu falsch berechneten Setzungen oder Tragfähigkeiten führen.

In der Regel geschieht die Modellierung des Boden-Bauteil-Kontakts durch das Mohr-Coulombsche Modell. Vorteil dieses Modells ist die einfache Handhabbarkeit durch wenige und überschaubare Parameter. Andere Modelle und mögliche Alternativen haben oftmals deutlich mehr Parameter, deren Einfluss auch nicht so einfach zu überblicken ist. Diese Einfachheit des Mohr-Coulombschen Modells ist sicher einer der Hauptgründe wieso es so häufig angewendet wird, weiterer Vorteil ist die universelle Anwendbarkeit auf fein- und grobkörnige Böden, die alternative Modelle in der Regel nicht bieten.

Im Rahmen dieser Arbeit wurde ein Alternativmodell zur Interfaceformulierung untersucht, welches auf dem hypoplastischen Stoffmodell nach von Wolffersdorff beruht. Ziel der Arbeit war eine Bewertung des Modells und ein Vergleich zum konventionellen Mohr-Coulombschen Modell.

Arbeitsumfang

Mit der hypoplastischen Interfacebeschreibung wurden monotone Scherversuche unter verschiedenen Randbedingungen, zyklische Scherversuche und ein Randwertproblem in Form eines Pfahlversuchs in einer Zentrifuge, jeweils aus der Fachliteratur nachgerechnet. Ausgewählte Versuche, vor allem das Randwertproblem, wurden vergleichend ebenfalls mit dem Mohr-Coulombschen (MC) Modell gerechnet.

Berechnungsergebnisse

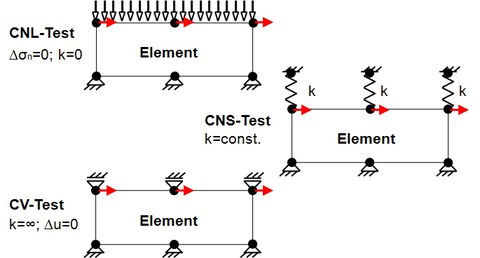
Bei Scherversuchen gibt es im Allgemeinen 3 mögliche Randbedingungen, die in Abbildung 1 dargestellt sind. Beim Constant-Normal-Load-Test (CNL) ist während der Scherung (rote Pfeile) im Element konstant die gleiche Normalspannung (σn) vorhanden, die oberen Knoten können sich in vertikaler Richtung verformen (u). Beim Constant-Volume-Test (CV) werden die vertikalen Verformungen durch die Randbedingung verhindert und damit steigen die Normal- und damit auch die Schubspannung sehr stark an. Die dritte Randbedingung ist die Mitte zwischen den beiden anderen und wird als Constant-Normal-Stiffness (CNS) bezeichnet. Hier wird die Normalsteifigkeit (k) durch Federn konstant gehalten und die Normalspannung kann sich abhängig von der vertikalen Verformung, ändern. Für die vertikalen Verformungen der oberen Knoten ist der CV-Test die untere und der CNL-Test die obere Grenze. Für die Normalspannungen entsprechend umgekehrt. Zwischen diesen beiden Grenzen bewegt sich der CNS-Test in Abhängigkeit der Normalsteifigkeit.

Monotone Scherung

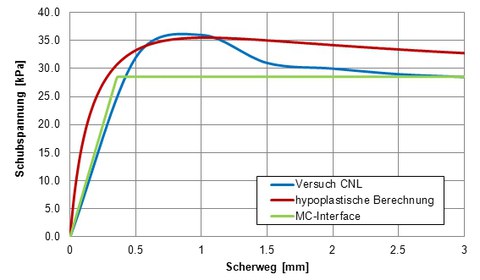
Bei den monotonen Versuchen wurde ein Model, ähnlich denen aus Abbildung 1 verwendet und dem Element die Eigenschaften des Interface zugewiesen. In Abbildung 2 sind das Ergebnis eines CNL-Versuchs und die Nachrechnungen für das MC- und das hypoplastische Interfacemodell für die Schubspannungen dargestellt. Das MC-Modell kann man über den Reibungswinkel nur auf den Peak- oder den Residualwert einstellen, was dem typischen bilinearen Verlauf entspricht. Mit dem hypoplastischen Modell kann man theoretisch den Verlauf aus dem Versuch nachzeichnen, allerdings ist der Abfall der Schubspannung im hypoplastischen Modell immer geringer als in Wirklichkeit.

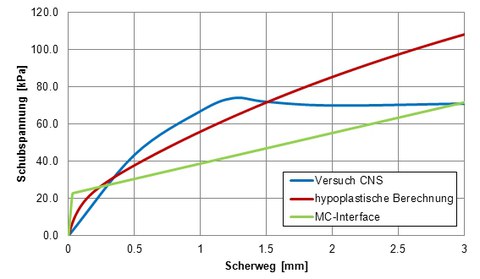
Die Ergebnisse aus Versuch und Nachrechnung für einen CNS-Versuch sind in Abbildung 3 dargestellt. Für kleine Scherverformungen (bis 1mm) kann die tatsächlich mobilisierte Schubspannung vom hypoplastischen Modell gut erfasst werden, bei größeren Verformungen ergeben sich aber Ungenauigkeiten. Für das MC-Modell gilt das analog, allerdings sind hier die Abweichungen bei geringer Scherung deutlich größer.

Zyklische Scherung

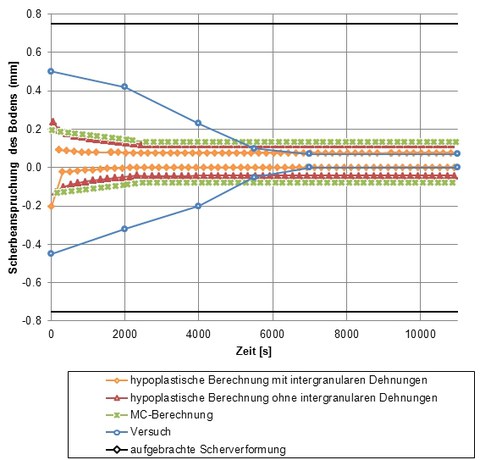
Die nachgerechneten zyklischen Scherversuche wurden ähnlich den monotonen Scherversuchen modelliert, da der Versuchsstand identisch war. Über dem Interfaceelement wurde hier noch eine Schicht, die den Boden darstellt, modelliert. Dies ist vor allem darin begründet, dass die absolut aufgebrachte Scherverformung zum Teil vom Interface und zum anderen Teil von Boden aufgenommen wird. Der Anteil vom Boden ist zu Beginn des Versuchs relativ groß (80%), nimmt bei zunehmender Anzahl an Zyklen aber ab und bei ausreichend langer Versuchsdauer ist dieser Anteil dann deutlich unter 10%. Die fehlenden Anteile bis 100% werden entsprechend vom Interface aufgenommen. Die Amplitude der zyklisch aufgebrachten Verformung beträgt 0,75mm und 1 Zyklus dauert 200s. Der Effekt der Aufteilung der Scherbeanspruchung ist in Abbildung 4, wo die Scherbeanspruchung des Bodens dargestellt ist, gut zu sehen. Die Nachrechnungen können diesen Effekt nur sehr begrenzt, wohl aber den Residualwert der Bodenscherbeanspruchung, wiedergeben. Bei dem hypoplastischen Modell wurden zusätzlich intergranulare Dehnungen berücksichtigt, die beim Wechsel der Belastungsrichtung eine zusätzliche Steifigkeit des Bodens oder des Interface berücksichtigen. Deshalb lieferte diese Berechnung auch die beste Übereinstimmung mit dem Residualwert.

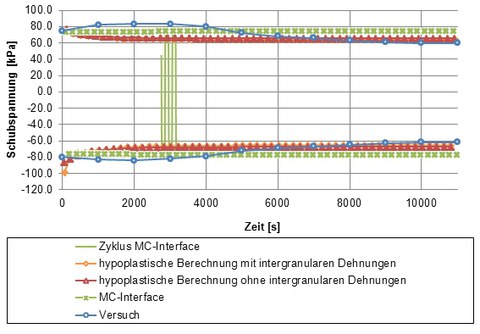
In Abbildung 5 sind für jeden Zyklus jeweils 2 Werte die maximale und die minimale Schubspannung aus Versuch und Nachrechnung dargestellt. Die mobilisierte Schubspannung bleibt bei den Nachrechnungen über die gesamte Versuchsdauer konstant, für die hypoplastischen Nachrechnungen liegt die errechnete Schubspannung sehr nah an den Residualwerten aus dem Versuch. Einen Peak- und Residualwert wie im Versuch gibt es aber bei allen Nachrechnungen nicht.

Randwertproblem (Zentrifugen Pfahlversuch)

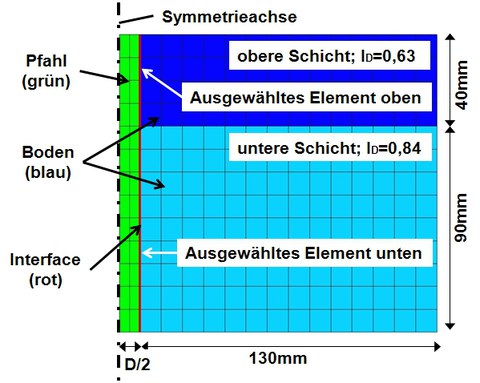
In Abbildung 6 ist das berechnete Randwertproblem einschließlich FE-Netz dargestellt. Es gibt 2 Bodenschichten und entsprechend wurde auch der Pfahl und das Interface in 2 Schichten unterteilt, die sich aber nur in Bezug auf die Lagerungsdichte des Bodens unterscheiden.

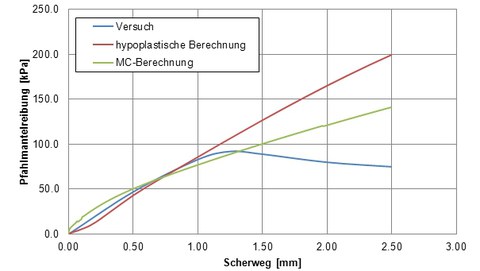
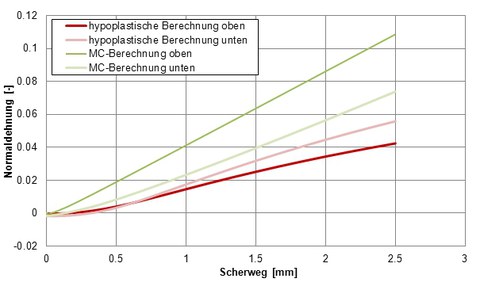
In den Versuchen wurden die Durchmesser des Pfahls (3, 5, 10, 18mm) und die Beschleunigungen in der Zentrifuge (30, 50, 100, 180*g) variiert. Belastet wird das System durch Eigenlast im erhöhten Schwerefeld und durch eine aufgebrachte Verschiebung des Pfahls um insgesamt 2,5mm nach oben. Theoretisch gleicht die Scherbeanspruchung des Interface bei diesem Versuch einem CNS-Test. In Abbildung 7 ist der Verlauf der Pfahlmantelreibung aus dem Versuch, der hypoplastischen und der Mohr-Coulombschen Nachrechnung während der Verschiebung des Pfahls zu sehen. Für den Bereich kleiner Scherverformungen stimmt das hypoplastische Modell mit der Versuchskurve sehr gut überein, bei größeren Verformungen weichen beide Modelle sehr stark ab, wenn auch das Mohr-Coulombsche Modell etwas bessere Ergebnisse liefert. Der Grund für die in den Nachrechnungen immer weiter ansteigende Schubspannung ist die Dilatanz im dicht gelagerten Interface und Boden, welche einen Anstieg der Normalspannung im Interface erzeugt. Die Normaldehnungen in ausgewählten Punkten (siehe Abbildung 6) ist in Abbildung 8 dargestellt.

Der Effekt, dass durch dilatantes Verhalten des dicht gelagerten Sandes die mobilisierten Schubspannungen immer weiter ansteigen, wird am Verlauf der Versuchskurve nicht deutlich, dort fallen nach Erreichen eines Peak-Wertes die Spannungen deutlich ab. Dies könnte auf Probleme bei der Versuchsdurchführung hindeuten, weshalb nur der Verlauf der mob. Mantelreibung bis zum Peakwert Aussagekräftig ist.

Zusammenfassung

Prinzipiell liefert das hypoplastische Modell bessere Berechnungsergebnisse als das herkömmliche MC-Modell. Vor allem bei größerer Scherverformung ergeben sich aber zum Teil sehr deutliche Abweichungen von realen Bodenverhalten, hingegen wird das Verhalten bei kleinen Scherverformungen sehr gut wiedergegeben. Das hypoplastische Modell ist bei der Handhabung der verwendeten Parametern einfacher und zuverlässiger als das Mohr-Coulombsche Modell, da die beim MC-Modell verwendete Parameter zum Teil nur eine rein mechanische, Bedeutung haben.

Für die Zukunft ist zu untersuchen ob die Abweichungen der Schubspannungen Modell- oder Versuchsbedingt sind und das Modell für größere Scherverformungen dahingehend zu verbessern ist. Das hypoplastische Modell ist nur für grobkörnige Böden anwendbar, was ein großer Nachteil gegenüber dem MC-Modell ist und daher ist es für die Zukunft sinnvoll zu prüfen ob eine Übertragung auf feinkörnige Böden möglich ist.

Bearbeitungszeitraum:

08/2010 – 11/2010

Wissenschaftliche Betreuer:

© Ulrich van Stipriaan

Head of Institute of Geotechnical Engineering

Name

Univ.-Prof. Dr.-Ing. habil. Ivo Herle

Head of Chair of Soil Mechanics and Foundation Engineering

Send email

Send encrypted email via the SecureMail portal (for TUD external users only).

Contact Information

Organization Name

Chair of Soil Mechanics and Foundation Engineering

Chair of Soil Mechanics and Foundation Engineering

Address work

Visiting address:

Neuffer-Bau (NEU), NEU 111 George-Bähr-Str. 1a

01069 Dresden

Show map of this location.

work Tel.

Office hours:

on appointment

Dr. Ing Michael Arnold