Modul 7 - Von der Aufzeichnung zur Anwendung - Bildverarbeitung - Digitale Bildverarbeitung - Geometrische Transformation
Geometrische Transformationen dienen nicht nur dazu, Verzerrungen durch das Aufnahme-System und das Geländerelief zu korrigieren, sondern auch um die Daten in ein geodätisches Referenzsystem, beispielsweise in ein Landeskoordinatensystem, einzupassen.
Dies lässt sich digital sehr einfach durchführen. Voraussetzung dafür sind im Bild sichtbare Passpunkte. Mit Hilfe dieser Punkte können die geometrischen Beziehungen zwischen Bild- und Geländefläche hergestellt, die Transformationsparameter berechnet und die Transformationsgleichungen aufgestellt werden. Danach kann die eigentliche Entzerrung, entweder mit Hilfe der direkten oder der indirekten Transformation, durchgeführt werden.
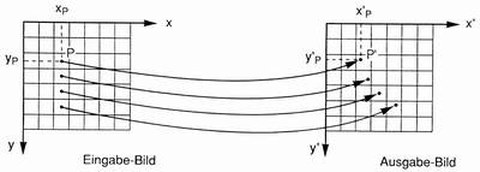
Bei der direkten Transformation wird für jedes Pixel des Eingabebildes seine Lage im Ausgabebild berechnet und der entsprechende Grauwert zugewiesen. Dabei kann es passieren, dass einzelne Pixel des Ausgabebildes mehrfach, andere gar nicht belegt werden und damit Informationen unter Umständen verloren gehen.
Abb. 7-3: Prinzip der direkten Transformation (aus Albertz, 1991)
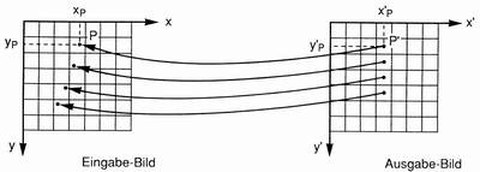
Diese Schwierigkeiten lassen sich mit der indirekten Transformation umgehen. Mit der Transformationsfunktion wird vom Ausgabebild, das erst entstehen soll, ins Eingabebild zurückgerechnet. Vom Eingabebild wird für jedes Pixel des Ausgabebildes der richtige Grauwert übernommen. Dadurch entsteht eine unmittelbar entzerrte Bildmatrix.
Abb. 7-4: Prinzip der direkten Transformation (aus Albertz, 1991)
Durch eine geometrische Transformation werden also die Daten des Eingabebildes in der für das Ausgabebild gewählten Matrix neu geordnet. Dies wird als Resampling bezeichnet.
Problematisch ist allerdings, wie aus voriger Abbildung zu ersehen ist, dass sich bei der Rückrechnung keine ganzzahligen Werte für die Bildkoordinaten x und y im Eingabebild, und damit genau genommen auch keine exakten Grauwerte, ergeben. Für die Grauwert-Zuweisung müssen also Regeln eingeführt werden. Dies sind im einzelnen die Methoden der nächsten Nachbarschaft, der bilinearen und der bikubischen Interpolation.
Bei der Methode der nächsten Nachbarschaft wird der Grauwert jenes Pixels im Eingabebild übernommen, welches den berechneten Koordinaten x und y am nächsten liegt. Dieses Verfahren wird verwendet, wenn die radiometrischen Informationen nicht verändert werden sollen.
Bei der bilinearen Interpolation bestimmt sich der Grauwert des Ausgabebildes zunächst ebenfalls über die Rücktransformation ins Eingabebild, um die Koordinaten x und y zu bestimmen. Danach wird der Grauwert über eine lineare Interpolation (Mittelwertbildung) der Grauwerte der 4 benachbarten Pixel berechnet und dem Pixel im Ausgabebild zugewiesen.
Die bikubische Interpolation funktioniert nach dem gleichen Prinzip, nur verwendet sie dementsprechend die Werte von 4 x 4 umliegenden Pixel, um den Grauwert zu bestimmen. Diese Methode liefert zwar die besten Ergebnisse, benötigt jedoch einen höheren Rechenaufwand.
Die Auswahl des Verfahrens bestimmt sich, wie schon erwähnt, durch den nötigen Rechenaufwand und den Anspruch an das Ergebnis, wobei bei dem heutigen und auch zukünftigen Entwicklungsstand der Rechentechnik der nötige Rechenaufwand eine immer unwesentlichere Rolle spielen wird.
| [zurück] | Analoge Bildverarbeitung |
| [weiter] | Radiometrische Korrekturen |
[Modul 1] [Modul 2] [Modul 3] [Modul 4] [Modul 5] [Modul 6] [Modul 7] [Modul 8] [Modul 9 ]
[Startseite] [Stichwortverzeichnis] [Literatur] [Impressum]