Mar 24, 2021
Revealing the Potential of Multi-Objective Optimization Problems
Most common optimization problems are multi-objective, i.e., one tries to simultaneously optimize several (usually conflicting) criteria at the same time -- for example, travel time vs. cost (for tickets, fuel, etc.) or optimal flight trajectory vs. best possible noise protection for residents. For researchers in this field (called multi-objective optimization), the biennial International Conference on Evolutionary Multi-Criterion Optimization provides one of the best opportunities to exchange new findings in this area.
At this year's edition of this conference series, the members of our newly founded Chair of Big Data Analytics in Transportation are represented with two publications:
- Lennart Schäpermeier, Christian Grimme, Pascal Kerschke (2021). To Boldly Show What No One Has Seen Before: A Dashboard for Visualizing Multi-objective Landscapes. In: International Conference on Evolutionary Multi-Criterion Optimization, 632-644, Springer.
- Pelin Aspar, Pascal Kerschke, Vera Steinhoff, Heike Trautmann, Christian Grimme (2021). Multi3: Optimizing Multimodal Single-Objective Continuous Problems in the Multi-objective Space by Means of Multiobjectivization. In: International Conference on Evolutionary Multi-Criterion Optimization, 311-322, Springer.
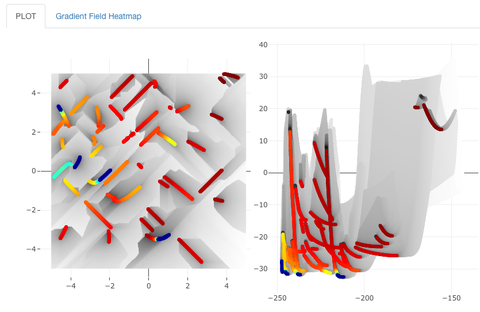
The core of the first publication is a dashboard that enables an interactive visual investigation of multi-objective optimization problems (with up to three input variables and/or target criteria). The dashboard allows the selection from various visualization methods and thus forms the currently most comprehensive and modern tool for the visual analysis of such problems.
The dashboard (along with all its visualization functionalities) can be explored at the following link: https://schaepermeier.shinyapps.io/moPLOT
Our second conference paper is about using multi-objective optimization algorithms to optimize single-objective problems. In contrast to the common assumption that problems become harder with increasing number of objectives, we could observe (using our visualization methods) that some problem properties become "friendlier" (from an algorithmic point of view) with increasing number of objectives. We investigated (and confirmed) our observation using experimental studies.