Das Potential mehrkriteriel­ler Optimierungs­probleme

Die meisten gängigen Optimierungsprobleme sind mehrkriteriell, d.h. man versucht gleichzeitig mehrere (zumeist konfliktäre) Kriterien gleichzeitig zu optimieren -- beispielsweise Reisezeit vs. Kosten (für Tickets, Kraftstoff, etc.) oder optimale Flugroute vs. bestmöglicher Lärmschutz für Anwohner. Für Forschende in diesem Themenfeld (der sogenannten mehrkriteriellen Optimierung) bildet die alle zwei Jahre stattfindende  International Conference on Evolutionary Multi-Criterion Optimization eine der besten Gelegenheiten zum Austausch neuer Erkenntnisse auf diesem Gebiet.

Bei der diesjährigen Edition dieser Konferenzreihe sind die Mitarbeiter des frisch gegründeten Lehrstuhls für Big Data Analytics in Transportation gleich mit zwei Pubklikationen vertreten:

• Lennart Schäpermeier, Christian Grimme, Pascal Kerschke (2021). To Boldly Show What No One Has Seen Before: A Dashboard for Visualizing Multi-objective Landscapes. In: International Conference on Evolutionary Multi-Criterion Optimization, 632-644, Springer.
• Pelin Aspar, Pascal Kerschke, Vera Steinhoff, Heike Trautmann, Christian Grimme (2021). Multi³: Optimizing Multimodal Single-Objective Continuous Problems in the Multi-objective Space by Means of Multiobjectivization. In: International Conference on Evolutionary Multi-Criterion Optimization, 311-322, Springer.

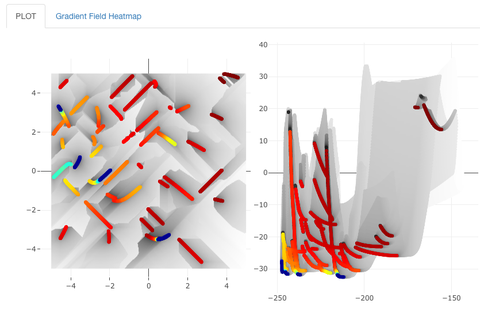
Den Kern der ersten Publikation bildet ein Dashboard, welches eine interaktive visuelle Untersuchung mehrkriterieller Optimierungsprobleme (mit bis zu drei Einflussgrößen und/oder Zielkritierien) ermöglicht. Das Dashboard ermöglicht die Auswahl aus diversen Visualisierungsmethoden und bildet dadurch das derzeit umfangreichste und modernste Tool zur visuellen Analyse solcher Probleme. 
Das Dashboard (mitsamt all seinen Visualisierungsmöglichkeiten) kann unter folgendem Link ausprobiert werden: https://schaepermeier.shinyapps.io/moPLOT

In unserem zweiten Konferenzbeitrag geht es um die Verwendung mehrkriterieller Optimierungsalgorithmen zur Optimierung einkriterieller Probleme. Im Gegensatz zur gängigen Annahme, dass Probleme mit steigender Anzahl an Zielgrößen schwerer werden, konnten wir (mit Hilfe unserer Visualisierungsmethoden) beobachten, dass einige Problemeigenschaften mit steigender Anzahl an Zielgrößen (aus algorithmischer Sicht) "freundlicher" werden. Unsere Beobachtung haben wir mit Hilfe experimenteller Studien untersucht (und bestätigt).