14.11.2023
Neue Publikation in "Omega"
Wir freuen uns über eine neue Veröffentlichung unter Beteiligung unseres Lehrstuhl in der Zeitschrift "Omega" mit dem Titel "Historical information based iterated greedy algorithm for distributed flowshop group scheduling problem with sequence-dependent setup times". Diese ist aus einer Zusammenarbeit von Janis Neufeld mit den Kollegen Xuan He, Qan-Ke Pan (beide Shanghai University), Liang Gao (Huazhong University of Science & Technology, Wuhan) sowie Jatinder N.D. Gupta (University of Alabama, Huntsville) entstanden. Die Publikation befasst sich der Minimierung der Gesamtdurchlaufzeit in Distributed Flow Shop Scheduling Problemen, d.h. der Maschinenbelegungsplanung in Produktionsnetzwerken mit Fließfertigung. Dabei wird ein innovativer Iterated Greedy-Algorithmus vorgestellt, der Lösungen auf der Grundlage historischer Informationen, die während des Lösungsprozesses gewonnen werden, verbessert.
Die Publikation kann unter folgender Internetadresse bis zum 01. Januar 2024 kostenlos abgerufen werden:
https://authors.elsevier.com/c/1i4Rf15N2OxeqF
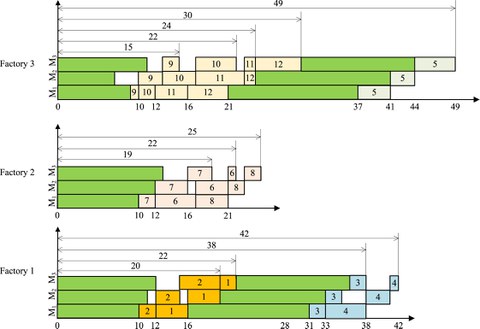
Abstract
Distributed flowshop group scheduling problem (DFGSP) is commonly seen in modern industry. However, research works on DFGSP with total flow time criterion are rarely reported. The DFGSP consists of three coupled sub-problems, i.e., factory assignment for each group, group sequence in each factory, and job sequence within each group. A historical information-based iterated greedy algorithm (HIG) is proposed for solving the DFGSP with the objective of minimizing total flow time. The HIG integrates an iterated greedy algorithm (IG) with a group-based insertion operator, a job-based insertion operator, a domination criterion-based swap operator, and a historical information-based constructive solution method. The domination criterion is an effective inequality, which can deterministically optimize the objective value of a partial sequence even if the scheduling sequence of subsequent jobs is unknown. In the constructive solution method, a set covering model is designed to capture the effective factory allocation patterns for the groups hidden in the historical solutions to speed up the search for the IG. The comprehensive experiments on 810 test instances demonstrate the effectiveness of HIG.