Nov 14, 2023
New Publication in "Omega"
We are pleased to announce a new publication with the participation of our chair in the "Omega" entitled "Historical information based iterated greedy algorithm for distributed flowshop group scheduling problem with sequence-dependent setup times". It is a joint work of Janis Neufeld and the colleagues Xuan He, Qan-Ke Pan (both Shanghai University), Liang Gao (Huazhong University of Science & Technology, Wuhan), and Jatinder N.D. Gupta (University of Alabama, Huntsville). The publication addresses the distributed flow shop group scheduling problem with a focus on the total flow time criterion. It introduces an innovative iterated greedy algorithm that improves solutions based on historical informations that is gained during the solution process.
The publication can be accessed free of charge until January 1, 2024 via the following link:
https://authors.elsevier.com/c/1i4Rf15N2OxeqF
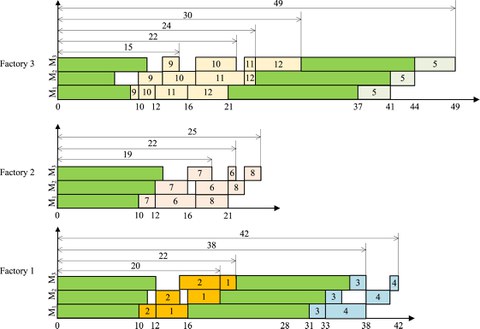
Abstract
Distributed flowshop group scheduling problem (DFGSP) is commonly seen in modern industry. However, research works on DFGSP with total flow time criterion are rarely reported. The DFGSP consists of three coupled sub-problems, i.e., factory assignment for each group, group sequence in each factory, and job sequence within each group. A historical information-based iterated greedy algorithm (HIG) is proposed for solving the DFGSP with the objective of minimizing total flow time. The HIG integrates an iterated greedy algorithm (IG) with a group-based insertion operator, a job-based insertion operator, a domination criterion-based swap operator, and a historical information-based constructive solution method. The domination criterion is an effective inequality, which can deterministically optimize the objective value of a partial sequence even if the scheduling sequence of subsequent jobs is unknown. In the constructive solution method, a set covering model is designed to capture the effective factory allocation patterns for the groups hidden in the historical solutions to speed up the search for the IG. The comprehensive experiments on 810 test instances demonstrate the effectiveness of HIG.