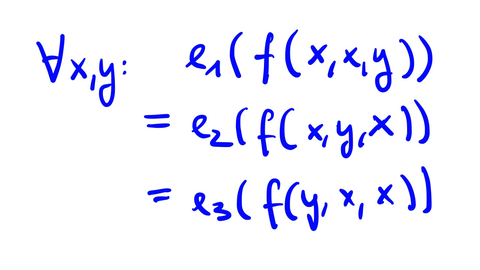Pseudo-Arc © M. Bodirsky

Forschung

Ein wichtiges aktuelles Forschungsthema am Lehrstuhl ist die Berechnungskomplexität von Constraint Satisfaction Problemen. Hierbei kommen universelle Algebra und Modelltheorie zum Einsatz.

mehr erfahren Forschung

Überblick

ERC © ERC
Forschungs­projekte
p © bodirsky
ERC consolida­tor grant "CSP infinity"
Flieger © Ja
Publikatio­nen
Phylo © M. Bodirsky
Forschungs­profil
Büro © M. Bodirsky

Aktuelle Forschungsge­biete

  • Klassische Modelltheorie
  • Endliche Modelltheorie
  • Universelle Algebra
  • Ramseytheorie, unendliche Permutationsgruppen, homogene Strukturen
  • Constraint Satisfaction Probleme: Algorithmen und Komplexität

Constraint Satisfaction Probleme sind Berechnungsprobleme, die in vielen Gebieten der theoretischen Informatik eine wichtige Rolle spielen. Ziel des Projektes ist, die Berechnungskomplexität von Constraint Satisfaction Problemen (CSPs) auf unendlichen Wertebereichen besser zu verstehen: welche CSPs lassen sich mit effizienten Algorithmen lösen, und für welche CSPs geht das nicht? Hierbei kommen Techniken und Resultate aus der universellen Algebra, der Modelltheorie, und der Ramseytheorie zum Einsatz. 

Hier eine aktualisierte Version meines Buches mit dem Titel "Complexity of Infinite-Domain Constraint Satisfaction", welches in der LNL Serie (Cambridge University Press) erschienen ist.