Dynamical processes in atoms, molecules and solids
Approximation of partial barriers in Hamiltonian systems
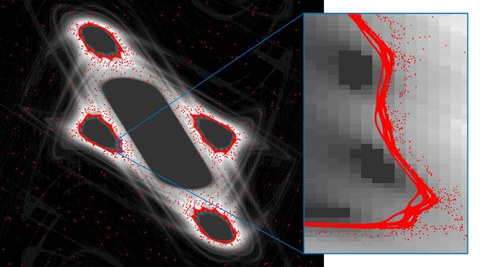
Hamiltonian systems typically exhibit a mixed phase space, with regions characterized by regular and chaotic behavior, respectively. Such dynamically distinct regions may be separated completely by invariant curves or surfaces. Additionally, there exist partial barriers. These barriers are permeable but hard to cross for trajectories (see figure), and thus they significantly influence the transport properties of the underlying system. While in 2D systems the mechanism is well understood, in higher-dimensional systems these observations need to be investigated more precisely. To get a better understanding of these transport processes, we will pursue a computational approach. Our goal is to obtain a highly resolved numerical approximation of partial barriers. To this end, we study the system by means of hierarchical partitions of the phase space and concepts from the ergodic theory within a set-oriented numerical framework.
This allows us to largely avoid observing some “typical” long trajectories. Instead, we will describe the dynamics probabilistically based on a numerical approximation of a transfer operator in terms of a stochastic transition matrix. Spectral properties of this matrix are known to relate to transport properties of the underlying system and we will extend these concepts both theoretically and computationally to study the specific transport mechanism induced by partial barriers. Since the assembling of such a transition matrix is highly parallelizable and eigenvector computations mostly rely on matrix-vector-multiplications, an efficient (high-performance) GPU implementation is desirable.
Project duration: 05/2011 -
Funded by: International Max Planck Research School