Simulation von RT-CVD für Graphen und andere zwei-dimensionale Materialien
Das epitaktische Wachstum von Graphen wird sowohl durch die Interaktion mit dem Substrat als auch durch Thermodynamik, Kinetik und Prozessparameter bestimmt. Das führt zu einer Vielfalt von Wachstumsmustern und Defekten. Z. B. können Graphen-Inseln dendritisch oder sechseckig sein oder auch in der Form von Schmetterlingen wachsen. Kürzlich wurde festgestellt, dass die Formen durch ein anisotropes Phasenfeldmodell simuliert werden können. Durch geschicktes Wählen der anisotropen Diffusionskonstanten und Stufenenergie konnten die Formen von Graphen-Inseln auf verschiedenen Substraten nachvollzogen werden.
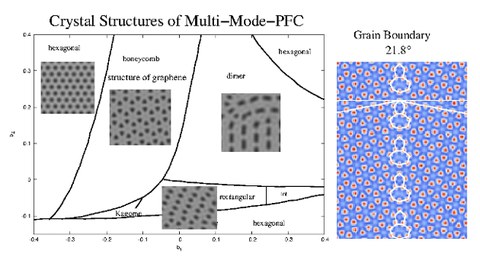
Wir schlagen ein erweitertes Phase-Field-Crystal (PFC) Modell vor. In einem PFC-Modell ist die Anisotropie der Stufenenergie und Diffusion aufgrund der Interaktion mit dem Substrat implizit bestimmt. Um die Graphen-Struktur mit einem PFC-Modell abzubilden, muss eine Multi-Mode-Erweiterung für PFC (MMPFC) genutzt werden. In MMPFC kann eine Vielzahl von zweidimensionalen Kristallstrukturen abgebildet werden, z. B. sechseckige, wabenförmige und rechteckige Strukturen. Die Beschreibung des Graphen als eine Dichtewelle führt zu einer natürlichen Einbeziehung von Defekten im Graphen und elastische Spannung aufgrund der Kopplung mit dem Substrat.
MMPFC muss weiterhin zu einem Modell erweitert werden, welches die Gasphase(VMMPFC) enthält, um die Phasengrenze besser kontrollieren zu können. Unser Ziel ist es, die Modellparameter einheitlich abhängig von der Interaktionsstsärke von Graphen mit dem Substrat zu definieren
Dadurch hoffen wir eine Modellbeschreibung des epitaktischen Wachstums von Graphen zu erlangen, in der die gesamte Anisotropie implizit durch die Struktur und die Kopplung vom Substrat zum Graphen beschrieben wird und nicht explizit ausgewählt werden muss wie im PF-Modell.
Projektlaufzeit: 10/2015 - 09/2018
Drittmittelgeber: ESF-Nachwuchsforschergruppe "Computer-Simulationen für das Materialdesign" (CoSiMa) vorgeschlagen vom Dresden Center for Computational Materials Science (DCMS), welches vom support-the-best Programm im Rahmen des Zukunfskonzeptes der TU Dresden gefördert wird