Hauptseminar Theoretische Physik
Frustrierter Magnetismus
Zeit/Ort
Mittwoch, 11:10h-12:40h, BZW/A120
Vorbesprechung und Themenvergabe: Mi 03.04.2019
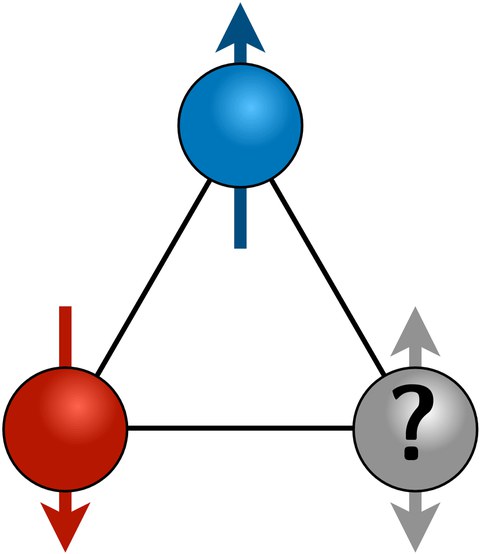
Magnetismus beruht auf der Wechselwirkung zwischen magnetischen Momenten (Spins) in Festkörpern. Dabei bezeichnet Frustration eine Situation, in der nicht alle Beiträge zur Wechselwirkungsenergie gleichzeitig minimiert (alternativ: nicht alle Randbedingungen gleichzeitig erfüllt) werden können. Ein einfaches Beispiel zeigt die Skizze: Für eine antiferromagnetische Wechselwirkung zwischen den durch Pfeile angedeuteten Spins ist eine antiparallele Ausrichtung energetisch bevorzugt. Entlang aller Seiten eines Dreieckes ist dies jedoch nicht gleichzeitig möglich.
Frustration unterdrückt i.a. konventionelle magnetische Zustände (wie Ferromagnetismus oder Antiferromagnetismus) und führt stattdessen zu neuartigen Zuständen, die durch komplizierte Formen von Ordnung und/oder durch topologische Eigenschaften gekennzeichnet sind.
Frustrierter Magnetismus ist eines der aktivsten Forschungsgebiete der modernen Festkörperphysik, in dem fundamentale Fragen nach der Natur von Materiezuständen und deren Anregungen gestellt werden. An der TU Dresden ist in Zusammenarbeit mit mehreren DRESDEN concept-Partnern der Sonderforschungsbereich 1143 diesem aktuellen Thema gewidmet.
Themenvorschläge
- Magnetismus von Isolatoren: Modelle, Symmetrien, Spin-Bahn-Kopplung, etc.
- Klassische Heisenberg-Modelle mit konkurrierenden Wechselwirkungen
- Spinwellentheorie und unterdrückte Ordnung
- Quantenphasenübergänge: Ising-Kette im transversalen Feld
- Spin-Flüssigkeiten: Überblick, resonating valence bonds, etc.
- Ising-Modell auf dem Dreiecksgitter
- Spin-Eis und magnetische Monopole
- Frustration durch Anisotropie: Kitaev-Modell auf dem Honigwabengitter
- Shastry-Sutherland-Modell
- Heisenberg-Modell auf dem Kagome-Gitter
- Spin-Flüssigkeiten: Materialien und Experimente
- Spin-Gläser
- Frustrierter Magnetismus in Metallen
Literatur
- R. Moessner and A. P. Ramirez, Geometrical frustration, Physics Today 59 (2), 24 (2006).
- A. P. Ramirez, Strongly Geometrically Frustrated Magnets, Annu. Rev. Mater. Sci. 24, 453 (1994).
- M. F. Collins and O. A. Petrenko, Triangular antiferromagnets, Can. J. Phys. 75, 605 (1997).
- C. Castelnovo, R. Moessner, and S. L. Sondhi, Magnetic monopoles in spin ice, Nature 451, 42 (2008).
- K. Binder and A. P. Young, Spin glasses: Experimental facts, theoretical concepts, and open questions, Rev. Mod. Phys. 58, 801 (1986).
- B. S. Shastry and B. Sutherland, Exact ground state of a quantum mechanical antiferromagnet, Physica 108B+C, 1069 (1981); J. Dorier, K. P. Schmidt, and F. Mila, Theory of Magnetization Plateaux in the Shastry-Sutherland Model, Phys. Rev. Lett. 101, 250402 (2008).
- L. Balents, Spin liquids in frustrated magnets, Nature 464, 199 (2010).