Forschung: Dirac-Kegel auf Wanderschaft

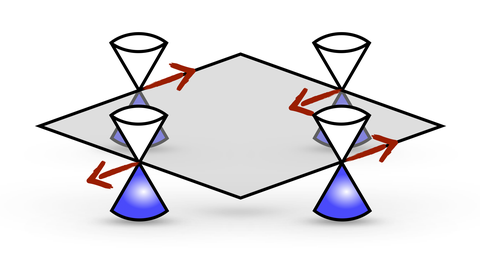
Topologische Halbmetalle sind elektronische Systeme in denen geschützte Bandkreuzungen, wie etwa Weyl- oder Dirac-Kegel, an isolierten Punkten in der Brillouin-Zone auftreten. In vielen Fällen sind die Positionen dieser Bandkreuzungen durch Symmetrien festgelegt.

Forschung im Rahmen des SFB 1143 in Zusammenarbeit mit der Julius-Maximilians-Universität Würzburg hat nun ein Beispiel eines stark korrelierten Dirac-Systems identifiziert, in dem die Symmetrie, welche die Positionen der Dirac-Kegel fixiert, bei tiefen Temperaturen spontan gebrochen wird. Dies führt dazu, dass sich die Dirac-Kegel innerhalb der Brillouin-Zone bewegen können. Mithilfe von umfangreichen Quanten-Monte-Carlo-Simulationen und einer begleitenden feldtheoretischen Analyse konnte der dazugehörige Quanten-Phasenübergang als ein neuartiger quantenkritischer Punkt identifiziert werden.

Diese Ergebnisse könnten für das Verständnis von d-Wellen-Hochtemperatur-Supraleitern und anderen stark korrelierten Materialen von Bedeutung sein.

J. Schwab, L. Janssen, K. Sun, Z. Y. Meng, I. F. Herbut, M. Vojta, F. F. Assaad,
Nematic Quantum Criticality in Dirac Systems,
Phys. Rev. Lett. 128, 157203 (2022)