Sep 07, 2020
Research: Pyrochlore S=1/2 Heisenberg antiferromagnet at finite temperature
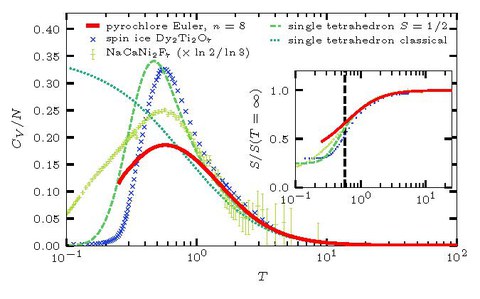
Figure 1 depicts our results pertaining to specific heat (red line, pyrochlore Euler, n=8) and entropy (in the inset) in the thermodynamic limit and compares it to experimental data of a spin 1 compound with very good quantitative agreement.
The three-dimensional pyrochlore lattice appears in various natural crystals like NaCaNi2F7.
Quantum pyrochlore magnets are extremely complex and theoretically challenging in particular due to the difficulty of performing reliable finite size scaling and the exponential growth of computational complexity with the number of lattice sites. Hence, many questions, concerning the low temperature and ground state physics remain unanswered.
The characteristic feature of the lattice is its tetrahedral unit cell, which induces strong geometrical frustration in combination with anti-ferromagnetic couplings, typical in quantum magnets.
Therefore, not all competitive exchange couplings can be satisfied simultaneously and the system is unable to determine a unique state of minimal energy, leading to a highly degenerate ground state in the classical case.
In our work, we combine state-of-the-art algorithms and large-scale numerical analysis to examine the finite temperature properties of the quantum (S=1/2) pyrochlore antiferromagnet. Using a systematic cluster expansion based on tetrahedra, we gain insights into its thermodynamic properties such as energy, specific heat, magnetization and entropy. Figure 1 depicts our results pertaining to specific heat (red line, pyrochlore Euler, n=8) and entropy (in the inset) in the thermodynamic limit and compares it to experimental data of a spin 1 compound with very good quantitative agreement.
R. Schäfer, I. Hagymási, R. Moessner, D. J. Luitz,
Pyrochlore S=1/2 Heisenberg antiferromagnet at finite temperature,
Phys. Rev. B 102, 054408 (2020)
