Research: Infinite Berry Curvature of Weyl Fermi Arcs

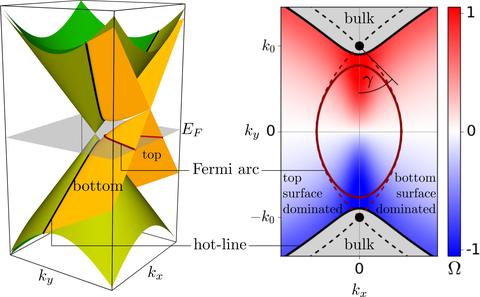
The Berry curvature (BC) of electronic bands in a solid is known to deeply influence a variety of material properties and phenomena. A well-known example of divergent BC is found in Weyl semimetals (WSMs) where two bands of the bulk electronic structure linearly touch at a point giving rise to a Weyl cone and to a BC hot-spot around this point. Less known is what happens at the surface of WSMs, in particular regarding the  topologically protected Fermi arcs. In our work, we show that Fermi arcs are generically accompanied by a divergence of the BC along a whole "hot-line", whenever the Weyl cone is tilted toward the surface of interest.

Typically, BC divergences reflect a rapid change of the intra-cell wave functions as the crystal momentum changes. In the case of a WSM slab here considered, the localization of the wave functions emerges as a critical aspect of the wave functions and, in fact, the BC hot-line separates the states localized on the surface from the continuum of 3D bulk states.

The large surface enhancement of the BC is expected to manifest in a variety of physical effects. In particular, the dipole moment of the BC of the Fermis arc will give rise to a gigantic contribution to the BC-driven non-linear Hall effect, which we find to grow linearly with the thickness of the WSM slab. Remarkable, this could even be observed in systems where the bulk BC dipole vanishes.

D. Wawrzik, J.-S. You, J. I. Facio, J. van den Brink, I. Sodemann,
Infinite Berry Curvature of Weyl Fermi Arcs,
Phys. Rev. Lett. 127, 056601 (2021) (arXiv)