Jan 08, 2024
Research: Phonon Topology and Winding of Spectral Weight in Graphite
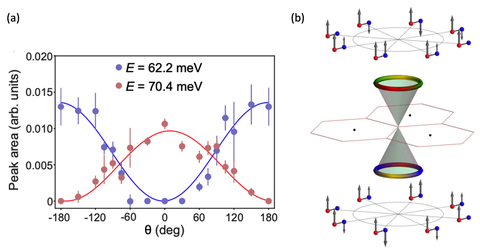
(a) Modulation of the inelastic X-ray scattering intensity on closed paths around the (pseudo-) Dirac point, above and below the gapped crossing at 67 meV. (b) This “winding of spectral weight corresponds to a continuous variation of the phase shifts between out-of-plane fluctuations of the two carbon sublattices (red/blue spheres).
Quasiparticle spectra of graphene are well known for their linear band crossings, which are attributable to the two-atomic basis of the honeycomb structure. This mechanism of non-trivial topology is independent of quantum statistics: Dirac-like band crossings occur not only in the electronic band structure but also in the dispersion of lattice fluctuations. In graphite, the finite coupling between carbon sheets locally breaks the inversion symmetry and necessarily gaps out such phonon (pseudo-) Dirac points. Previous momentum-resolved spectroscopic studies of bosonic band crossings suggested that an intensity modulation on a closed path in momentum space would directly measure the enclosed topological winding number (Berry charge). Using a combination of inelastic x-ray scattering and density functional theory, here we show that this is not strictly true: Even in a gapped system like graphite, a scan around the pseudo-Dirac crossing yields a clean modulation. We illustrate that this modulation encodes the variation of phase shifts between the two carbon sublattices performing out-of-plane fluctuations. Rather than being a clear indicator of a Dirac point, these topological-like lattice dynamics are observed in a characteristic range around the crossing, even if it is gapped.
N. D. Andriushin, A. S. Sukhanov, A. N. Korshunov, M. S. Pavlovskii, M. C. Rahn, S. E. Nikitin,
Phonon Topology and Winding of Spectral Weight in Graphite,
Phys. Rev. Lett. 131, 246601 (2023) (arXiv)
