May 12, 2022
Research: Screw dislocations in chiral magnets
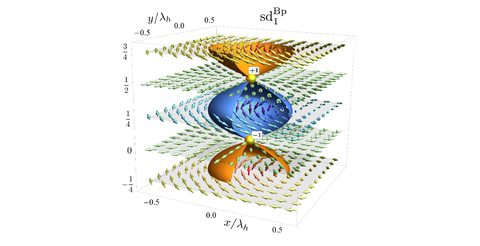
Screw dislocation line defect of helimagnetic order whose core contains Bloch point singularities (yellow spheres).
Dislocations are common defects of crystalline order whose topological character is specified by the Burgers vector. A particular case are crystals that are only spatially modulated along a single direction. Such lamellar order can be found in soft matter, e.g. smectic and cholesteric liquid crystals, but also in the solid state. For example, in chiral magnets like MnSi or Cu2OSeO3 the magnetization can vary in a helical fashion along a single spatial direction realizing an example of lamellar ordering. In three dimensional helimagnets dislocations are line defects. Depending on the mutual orientation of the dislocation line and its Burgers vector, one can distinguish between edge and screw dislocations. Up to now only edge dislocations defects of helimagnetic order have been reported.
The properties of screw dislocations of helimagnetic ordering was revealed in a recent theoretical study of our CRC. Whereas the far-field of these screw dislocations is universal and typical of lamellar ordering, it was found that a rich variety of dislocation-core structures can be realized. In particular, the micromagnetic core of screw dislocations can be either smooth or contains Bloch point singularities at which the amplitude of magnetization vanishes. In general, they also carry a non-integer but finite skyrmion charge suggesting that they can be efficiently manipulated with the help of spin currents.
Interestingly, screw dislocations are generically expected to occur at twist grain boundaries that separate two helimagnetic domains with different orientations of the helix axis. Such domain walls will naturally occur in the zero-field cooled state of chiral magnets but so far have not been identified experimentally. Twist grain boundaries are therefore a prime candidate for spotting screw dislocations in the experiment.
M. Azhar, V. P. Kravchuk, M. Garst,
Screw Dislocations in Chiral Magnets,
Phys. Rev. Lett. 128, 157204 (2022) (arXiv)
