07.02.2020
Abhängig oder nicht abhängig? Das ist hier die Frage. An der TU Dresden entwickelte statistische Methode ermöglicht das Erkennen beliebiger Abhängigkeitsstrukturen
Mathematiker Dr. Björn Böttcher von der TU Dresden stellt in dem Eröffnungsartikel des neuen Fachjournals „Open Statistics“ die Erweiterung der durch ihn und seine Kollegen entwickelten statistischen Kennzahl der "distance multivariance“ vor. Dabei wird gezeigt, dass die Theorie der "distance multivariance“ nicht nur eigenständig effektiv ist, sondern eine umfassende Theorie darstellt, die mehrere klassische Abhängigkeitsmaße vereinigt. Zusammenhänge zwischen zwei oder mehr hochdimensionalen Variablen können so erfasst und auch komplizierte nichtlineare Abhängigkeiten sowie Abhängigkeiten höherer Ordnung erkannt werden. Für zahlreiche wissenschaftliche Disziplinen eröffnet diese Methode neue Ansätze und Berechnungsmöglichkeiten, um Abhängigkeiten aufzudecken und zu bewerten.
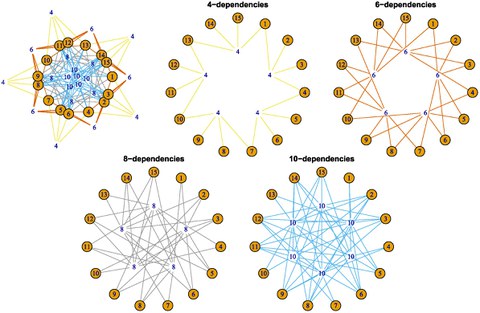
Vollständige Abhängigkeitsstrukturen
Lässt sich die Anzahl an Schulfehltagen mit dem Alter, dem Geschlecht oder der Herkunft der Schüler in Zusammenhang bringen? In einer Befragung mit 146 Schülerinnen und Schüler haben Sozialwissenschaftler verschiedene Einflussgrößen auf Schulfehltage analysiert und auf Abhängigkeiten untersucht, um daraus ein Vorhersagemodell ableiten zu können. Zu dieser klassischen Fragestellung gibt es verschiedene, breit diskutierte Herangehensweisen.
Das an der TU Dresden entwickelte Abhängigkeitsmaß "distance multivariance“ bietet zu diesem Problem einen komplett neuartigen Lösungsansatz: Dr. Björn Böttcher vom Institut für Mathematische Stochastik konnte mit Hilfe der "distance multivariance“ für dieses Beispiel den kulturellen Hintergrund sowie eine Abhängigkeit höherer Ordnung zu Alter und Geschlecht als Einflussgrößen für die versäumten Tage ermitteln. Daraus lässt sich zumindest ein Minimalmodell für die Anzahl der versäumten Tage ableiten. „Dieses ist ein elementares Beispiel für eine Anwendung der entwickelten Methode. Ob dies im Hinblick auf das Untersuchungsgebiet auch ein inhaltlich fundierter Befund ist, kann ich nicht beurteilen. Das Arbeiten mit Daten aus der Anwendung und insbesondere die fachspezifische Einordnung der Ergebnisse benötigt stets auch die Expertise aus dem jeweiligen Fach“, betont Dr. Böttcher und liefert in seinem Artikel zahlreiche weitere illustrative Beispiele für den Einsatz seiner Methode:
„In der Arbeit verweise ich auf über 350 frei verfügbare Datensätze aus verschiedensten Fachdisziplinen, in denen statistisch signifikante Abhängigkeiten höherer Ordnung auftreten. Auch hier gilt: Ob diese Abhängigkeiten im Sinne der jeweiligen Datenerhebung sinnvoll sind, bedarf weiterer Untersuchungen sowie fachliches Wissen im jeweiligen Gebiet, welches jenseits meiner Expertise ist“ und er ergänzt „selbstverständlich sind Anfragen zur Kooperation stets willkommen.“
Statistische Analysen betrachten üblicherweise Abhängigkeiten zwischen einzelnen Variablen. Insbesondere bei vielen Variablen kann es sinnvoll sein, zuerst zu untersuchen, welche Variablen überhaupt einen Einfluss haben, in anderen Worten, ob sie eine Abhängigkeit aufweisen. Dr. Björn Böttcher stellt dafür ein Verfahren unter dem Namen "dependence structure detection" (Erkennung von Abhängigkeitsstrukturen) vor, mit dem auch Abhängigkeiten höherer Ordnung entdeckt werden können. Abhängigkeiten höherer Ordnung bedeuten, dass obwohl jedes Variablenpaar unabhängig ist, mehr als zwei Variablen dennoch voneinander abhängen können. Abhängigkeiten dieser Art wurden in den meisten Anwendungen bisher nicht beachtet.
Einige Wissenschaftler vermuten, dass insbesondere in der Genetik Abhängigkeiten höher Ordnung vermehrt auftreten, diese konnten bisher nicht so einfach untersucht werden. Die Grundidee hierbei ist, dass mehrere Gene zusammen eine Eigenschaft bestimmen, diese Gene aber einzeln untereinander und jeweils einzeln mit der Eigenschaft keine Abhängigkeit aufweisen - somit würde tatsächlich eine Abhängigkeit höherer Ordnung vorliegen. Das Abhängigkeitsmaß "distance multivariance“ und das Verfahren "dependence structure detection" stellen nun vielversprechende Analyse-Werkzeuge für entsprechende Untersuchungen dar.
Für alle interessierten Anwender sind die hier vorgestellten Methoden im Paket ‚multivariance' für die freie Statistik-Software 'R‘ zur direkten Anwendung verfügbar.
Originalveröffentlichung:
B. Böttcher, Dependence and dependence structures: estimation and visualization using the unifying concept of distance multivariance, Open Statistics, Band 1, Heft 1, Seiten 1–46, ISSN (Online) 2657-3601, DOI: https://doi.org/10.1515/stat-2020-0001.
Informationen für Journalisten:
Dr. Björn Böttcher
Institut für Mathematische Stochastik
Tel.: 0351 463-32423

