Soil behaviour and constitutive models
The behaviour of soils is investigated in the laboratory by means of standardized tests, such as oedometric compression, direct shear or triaxial compression tests. However, using these tests not all stress paths, relevant for geotechnical problems, can be depicted. Special stress paths, e.g. characteristic for excavations, can only be modelled with triaxial setups having a computer controlled system or load control, as the cell pressure has to be regulated during the experiment.
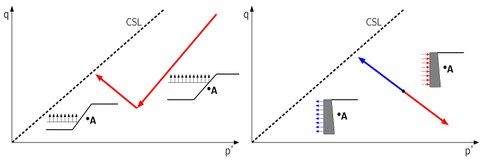
Stress paths representing geotechnical problems, left: excavation and right: activation of active and passive earth pressure
To predict deformations in major construction projects, for which analytical methods are not suitable, numerical calculations are used. An important part of a numerical calculation is the constitutive model, which represents the soil behaviour. Although there are different types of constitutive models, most of them can be calibrated with standard laboratory experiments.
Hypoplastic constitutive models belong to the group of advanced mathematical models for describing soil behaviour while loading. Compared to other constitutive models, hypoplastic models work without the use of flow surfaces and plastic potentials to reproduce reversible and irreversible strains. Instead, a value function is used. Since the soil behaviour of fine-grained and coarse-grained soils differs during loading, there are also different constitutive models that can reproduce the peculiarities of the two soil types.

Example for the numerical simulation of an uniaxial compression test with impeded lateral expansion. Simulation with a hypoplastic and linear-elastic—plastic constitutive model (Mohr-Coulomb model). The Mohr-Coulomb model cannot predict the soil behaviour during unloading.
Constitutive models use material parameters which have to be determined for every soil. The determination of the material parameters is carried out generally by means of laboratory experiments, see FAQ-Box 'Calibration of constitutive models'. In case there aren't any results available, correlations can also be used.
Constitutive models are mathematical models which are used to simulate numerically the soil behaviour for different loading scenarios. The constitutive models have a certain number of material parameters which vary for different soils. To predict deformations for geotechnical problems, e.g. settlements under a foundation, the material parameters must be calibrated initially

Oedometric compression device to analyse the compression behaviour of soils
The determination of the material parameters is carried out by means of standardized soil mechanical laboratory tests, such as uniaxial or isotropic compression tests, drained or undrained triaxial tests or direct shear tests.
With standard laboratory tests, the compression and shear behaviour of soils can be investigated experimentally. Subsequently, the laboratory tests are simulated with the help of numerical element tests. When simulating the experiments, the material parameters are adapted in order to obtain a measured and calculated deformation behaviour which is as similar as possible.

Determination of material parameters by means of results from undrained triaxial compression tests

Determination of material parameters by means of results from isotropic compression tests
Geotechnical element tests are laboratory tests on soil samples. The soil samples are considered to be homogeneous and a constant distribution of stress and strain is assumed in the sample. By means of these assumptions, during a laboratory test a snapshot of the state of the soil sample can be characterized with a single stress and strain tensor, i.e. the soil sample is considered as one single point. Thus, the soil sample represents one point in the ground. However, the inhomogeneity of the soil is neglected. Within a soil sample, an inhomogeneity is expressed e.g. by a different distribution of stiffness, void ratio, etc.
The calibration of constitutive models is carried out by means of a numerical simulation of the element tests. So far, all constitutive models have been developed neglecting the soil inhomogeneity described above.
At the Institute of Geotechnical Engineering, numerical simulations for the investigation of soil inhomogeneity in element tests were carried out. Assuming a normal distribution of the void ratio within the soil sample with defined mean value and normal deviation, the influence of the distribution of void ratio on the stress-strain behaviour can be investigated. The void ratio is distributed stochastically at various points.
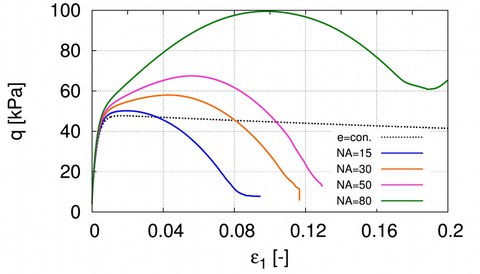
Influence of the normally distributed void ratio with different normal deviations on the stress-strain-behaviour for simulated triaxial compression tests
For some experimental test results, it is difficult to distinguish between the characteristic soil behaviour and abnormal effects, e.g. influences of soil sampling or the experimental device. Unexpected behaviour often leads to a repetition of the testing procedure in case sufficient sample material is available. The testing is carried out until the expected soil behaviour appears. However, the sample material or laboratory resources are limited most often. Thus, also the number of experiments are restricted.
At the Institute of Geotechnical Engineering, laboratory investigations have shown that the consideration of asymptotic conditions simplifies the interpretation of test results from triaxial compression tests on fine-grained soils. Here, the asymptotic states of the “Critical States Soil Mechanics” are considered. In the simplest case, the soil state is a snapshot of the density and the stresses, currently acting on a soil element. In theory, mainly state-independent parameters such as the critical friction angle φc or the compression or swelling coefficient (Cc, Cs) are used.
