T1: Origin of Flexibility and Mechanisms of Responsivity from first principles
Thomas Heine
The key question for understanding the flexibility in MOFs is to determine the individual contributions of the constituting building blocks to the MOF potential energy surface during phase switching. The principal components to the deformation energy are the strain energies associated with changes of the O-M-O angles of the DABCO-coordinated M2(O2C-R)4 (M = Mn, Co, Ni, Cu, Zn) paddle wheels (DCPW) and of the twisting of the linkers (R) in the O2C-R moieties, as well the London dispersion energy between the linkers. For this purpose we study pillared layer MOFs such as DUT-8, which is a prototypical example to study hinge energetics. An accurate description of the impact of the nature of the metal influencing the intrinsic flexibility and bi- or tri-stability of the node is solely achieved using first principle calculations. Calculating the individual components to the deformation energy and identifying metastable states on the potential energy surface of the deformed DCPWs is also a key ingredient for parameterizing force fields and grains in a multiscale method that is developed in collaboration with T2. In the first funding phase we found polymorphism in DUT-8(Ni) to play an important role in controlling switchability (Fig. 1). Two op-phases (A and B) varying in linker orientation around the PW are energetically quite similar, but only one of them (B) transforms into a dense cp-phase. A switching mechanism starting from A is therefore expected to traverse through an intermediate phase B before closing by linker rotation.
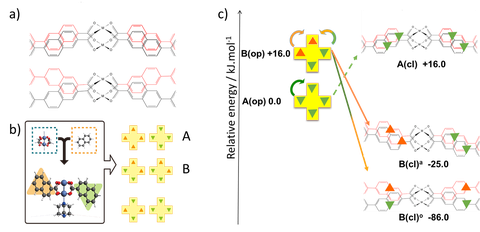
Fig. 1: The 2,6-ndc linker in DUT-8(Ni) gives rise to polymorphism in the op-form (A and B). For B isomers the op-cp transformation is energetically preferred.
P. S. Petkov, V. Bon, C. L. Hobday, A. B. Kuc, P. Melix, S. Kaskel, T. Düren, Th. Heine, “Conformational isomerism controls collective flexibility in metal–organic framework DUT-8(Ni)”, Phys. Chem. Chem. Phys. 2019, 21, 674-680 (doi: 10.1039/C8CP06600K).
A. Krylov, A. Vtyurin, P. Petkov, I. Senkovska, M. Maliuta, V. Bon, T. Heine, S. Kaskel, E. Slyusareva, "Raman spectroscopy studies of the terahertz vibrational modes of a DUT-8 (Ni) metal-organic framework", Phys. Chem. Chem. Phys. 2017, 19, 32099-32104 (doi: 10.1039/C7CP06225G).
