Mathematical modeling and numerical simulation of cells and systems
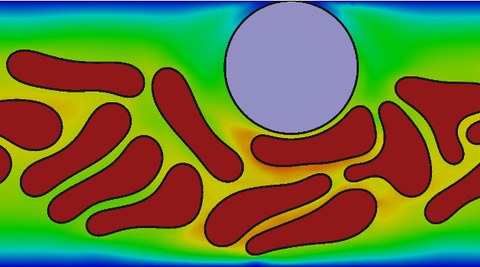
Cells are the smallest unit of life and are for itself of utmost complexity. Understanding the basic processes within a cell helps to understand life. A basic instrument of understanding those processes are mathematical models. In recent years, the simulation science supported by exponentially growing computer power made fundamental progress, giving rise to the development of more and more complex models. Within this project, we develop mathematical models for cells considered as multi-phase flow, with distinct physical properties of the cytoplasm of the cell and its extracelluar matrix separated by a membrane lipid bilayer. The physics of the cell membrane is described by a Helfrich hamiltonian and the cytoplasm is treated as a viscous or viscoelastic fluid or as a fluid liquid crystal. We apply this approach to cell motility, where we develop models for membrane protrusion and myosin contraction. In a further application, we focus on blood flow, where we investigate margination of white blood cells and demonstrate the dependency on a number of conditions including hematocrit, the deformability of the cells and the Reynolds number. To numerically treat the highly non-linear PDEs, we use and continuously advance the phase field method and our FEM toolbox AMDiS, allowing to solve arising equations with high performance computing.
Projektlaufzeit: 11/2012 - 10/2017
Drittmittelgeber: DFG