Research at the chair of Applied Analysis
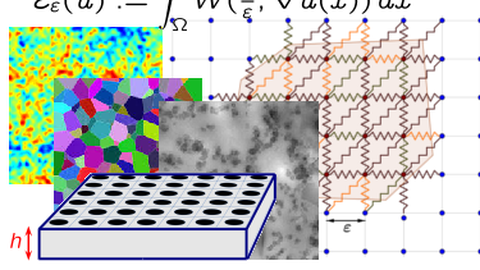
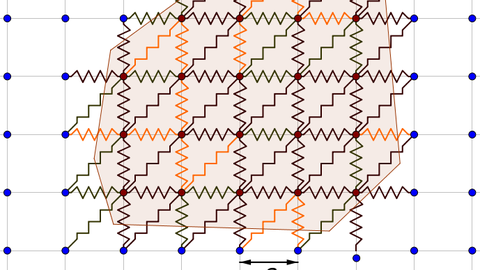
The behavior of many mathematical and physical models is determined by a complex interplay between multiple length, time and energy scales. This is for instance the case for microstructured materials that feature new and interesting properties on large length scales. Understanding the interplay of behaviors on different scales and predicting large-scale effective properties based on mathematical analysis (PDE-theory, Calculus of Variations, and homogenization theory) is one of our goals.
From micro to macro scales
The behavior of many mathematical and physical models is determined by a complex interplay between multiple length, time and energy scales. This is for instance the case for microstructured materials that feature new and interesting properties on large length scales.
In our research group we focus on the analysis and modeling of multiscale problems. A main motivation is to understand the interplay of behaviors on different scales and to predict large-scale effective properties based on methods from the theory of partial differential equations and the Calculus of Variations. We focus on models that feature multiple length scales, randomness, and nonlinearities. Often our problems live on the interface between applied analysis, continuum mechanics, probability theory, and sometimes are related to mathematical physics, see here.