scales © Stefan Neukamm

Research at the chair of Applied Analysis

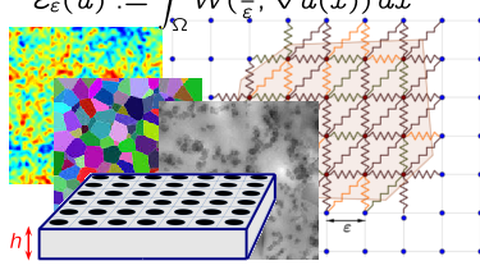
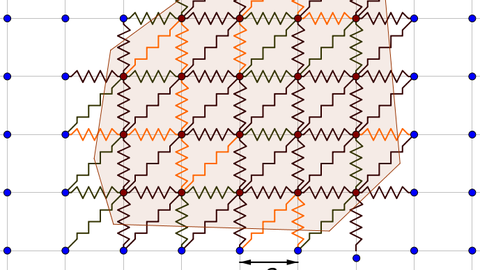
The behavior of many mathematical and physical models is determined by a complex interplay between multiple length, time and energy scales. This is for instance the case for microstructured materials that feature new and interesting properties on large length scales. Understanding the interplay of behaviors on different scales and predicting large-scale effective properties based on mathematical analysis (PDE-theory, Calculus of Variations, and homogenization theory) is one of our goals.

mehr erfahren Research at the chair of Applied Analysis

Unsere Forschung

Research Areas © Neukamm
Forschungs­felder

Our Research Areas
Random Field © S. Neukamm
Optimal homogeniza­tion rates in stochastic homogeniza­tion of nonlinear uniformly elliptic equations and systems

The paper "Optimal homogenization rates in stochastic homogenization of nonlinear uniformly elliptic equations and systems" by J. Fischer and S. Neukamm has been accepted for publication in ARMA.
helix © neukamm
Derivation of a homogenized bending-torsion theory for rods with micro-heteroge­neous prestrain

New preprint "Derivation of a homogenized bending-torsion theory for rods with micro-heterogeneous prestrain" (R. Bauer, S. Neukamm, M. Schäffner) available.
spring network © neukamm
Stochastic unfolding and homogeniza­tion of spring network models

Our paper "Stochastic unfolding and homogenization of spring network models" by S. Neukamm and M. Varga is accepted for publication in Multiscale Modeling and Simulation (SIAM).
Two-scale homogeniza­tion of abstract linear time-dependent PDEs

New preprint "Two-scale homogenization of abstract linear time-dependent PDEs" (Stefan Neukamm, Mario Vargam Marcus Waurick) is available.
Stochastic homogeniza­tion of Lambda-convex gradient flows

New preprint on "Stochastic homogenization of Lambda-convex gradient flows" (Martin Heida, Stefan Neukamm, Mario Varga) is available.
Uniform Lipschitz estimates in Nonlinear Elasticity

The paper "Lipschitz estimates and existence of correctors for nonlinearly elastic, periodic composites subject to small strains" (Stefan Neukamm, Mathias Schäffner) has been accepted in CVPDE.
Quantitati­ve Homogeniza­tion in Nonlinear Elasticity I

Our paper "Quantitative Homogenization in Nonlinear Elasticity for Small Loads" has been accepted for publication in ARMA.

From micro to macro scales

The behavior of many mathematical and physical models is determined by a complex interplay between multiple length, time and energy scales. This is for instance the case for microstructured materials that feature new and interesting properties on large length scales.

In our research group we focus on the analysis and modeling of multiscale problems. A main motivation is to understand the interplay of behaviors on different scales and to predict large-scale effective properties  based on methods from the theory of partial differential equations and the Calculus of Variations.  We focus on models that feature multiple length scales, randomness, and nonlinearities. Often our problems live on the interface between applied analysis, continuum mechanics, probability theory, and sometimes are related to mathematical physics, see here.