Jan 16, 2023
Research: Frozen Deconfined Quantum Criticality
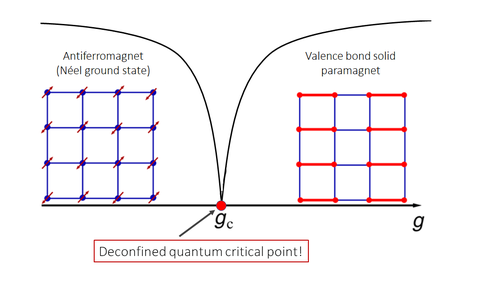
Schematic depiction of the phase diagram that features a deconfined quantum critical point in the two-dimensional easy-plane antiferromagnet we describe.
The nature of the phase transitions in quantum systems with competing order parameters has gained a lot of attention since the concept of the deconfined quantum criticality was introduced in 2004. It was then shown that a model describing a two-dimensional quantum antiferromagnet undergoes a second-order phase transition to a paramagnetic valence bond solid state. At the deconfined quantum critical point the order parameters describing both phases fall apart —deconfine— into more elementary particles called spinons. Monte Carlo simulations support the existence of the deconfined quantum critical point in SU(2) invariant systems, although the traditional Landau-Ginzburg-Wilson paradigm predicts a first-order phase transition. It was expected that deconfined quantum criticality arises in quantum antiferromagnets with easy-plane anisotropy as well. However, the numerics indicate instead a first-order phase transition.
In our findings we uncover the criticality of the easy-plane antiferromagnet described by the CP1 model starting from a regime analogous to the zero temperature limit of a certain classical statistical mechanics system which we therefore dub “frozen”. Through exact lattice duality transformations and renormalization group analysis we show that even in the regime with finite “temperature” the system flows to the same deconfined quantum critical point that is found in the frozen limit. As the dual to the easy-plane CP1 model theory we derive captures this critical behavior, we believe it can offer new insights for numerical studies of this well known system. Additionally, at criticality the theory acquires a topological order. Though this finding is interesting on its own, we use it to demonstrate that the bosonic theory we consider is dual to a fermionic one with two massless Dirac fermions, which thus undergoes a second-order phase transition as well.
V. Shyta, J. van den Brink, F. S. Nogueira,
Frozen Deconfined Quantum Criticality,
Phys. Rev. Lett. 129, 227203 (2022) (arXiv)
