Jan 09, 2024
Research: Continuous Phase Transitions between Fractional Quantum Hall States and Symmetry-Protected Topological States
Topological phases differ from conventional phases in that they cannot be described by local order parameters, and thus phase transitions between different topological phases also go beyond Landau’s symmetry breaking paradigm. It is therefore important to find and characterize continuous phase transitions between different topological phases.
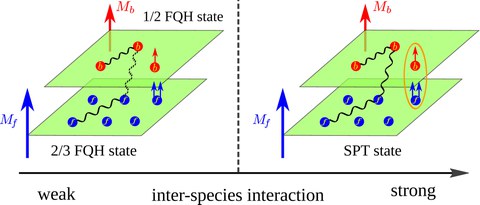
In this study, continuous quantum phase transitions between one symmetry-protected topological state and various fractional quantum Hall states in Bose-Fermi mixtures have been revealed. The transitions are described by Chern-Simons-Higgs theories which consist of Wilson-Fisher bosons coupled to emergent gauge fields. Numerical results suggest that the transitions are continuous and critical scaling of quantum entanglement is found. It is a rare example of continuous phase transition between symmetry-protected topological order and intrinsic topological order. This result opens a new avenue about quantum phase transitions between topological states.
Y.-H. Wu, H.-H. Tu, M. Cheng,
Continuous Phase Transitions between Fractional Quantum Hall States and Symmetry-Protected Topological States,
Phys. Rev. Lett. 131, 256502 (2023) (arXiv)