Research: Correlated quantum tunneling of monopoles in spin ice

The magnetism of rare-earth crystals can vary substantially depending on the chemical elements and the geometry of the lattice. A prominent characteristic of rare-earth ions is their sizeable spin-orbit coupling, and in magnetic pyrochlore oxides, despite similarities in structure, it leads to a wide variety of phenomena – spin glass, spin ice, and spin liquid are only a few examples of so called “exotic” phases. These arise because the natural tendency to develop long-range order is frustrated by the geometrical constraints of the crystal.

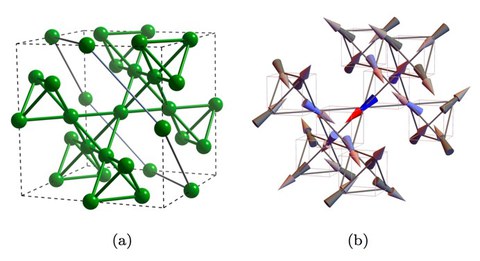
A system is said to be frustrated if competing interactions lead to conflicting classical minima in energy. In spin-ice the magnetic moments of the rare-earth ions, which sit at the vertices of a lattice of corner-sharing tetrahedra, are forced by the crystal fields to point along the axis joining adjacent tetrahedral centres. At temperatures of few kelvin, i.e. the order of spin-spin interactions, frustration and crystal field anisotropy favour correlated configurations with a degree of degeneracy which maps to the proton arrangement in water ice. Such spin configurations are summarised by the so called “ice rules”, which consist in having 2 spins per tetrahedron pointing toward its centre and the other 2 outward. These imply a ground state whose degeneracy scales with the size of the lattice. Excitations above the ground state correspond to local violations of the ice rules: they consist in tetrahedra hosting 3in-1out or 3out-1in spin-configurations. These “defects” are called magnetic monopoles because they act as sources and sinks of magnetization fluxes in the otherwise “vacuum” of the 2in-2out spin-background [2].

The dynamics and relaxation at low temperatures in spin-ice magnets is ascribed to quantum spin-tunnelling due to monopole hopping. Our theory therefore studies spin fluctuations originating from localised isolated monopoles. Our model is material-dependent, with the crystal-field Hamiltonian being the “foundation” for setting up the Hilbert space, and with the dipolar and exchange “building blocks” for interactions which allow dynamics and realistic estimation of timescales thereof.

Our central result is that there is a fundamental correlation between spin-dynamics, monopole excitations, and their local environment. Indeed, in the case of low densities of monopoles, whereas the vast majority of spins in the sample experience net longitudinal fields, those adjacent to a monopole have such longitudinal components suppressed. Moreover, the “same monopole” induces, statistically, a bimodal distribution of transverse fields. As transverse fields induce spin-tunnelling, these results imply that for a flippable spin next to a monopole, two very distinct rates,  t^fast and t^slow , appear, with a 2:1 ratio. The spin dynamics is therefore remarkably correlated to the local environment and the propagation of monopoles is intrinsically stochastic. Contrary to conventional modelling that assumes a uniform distribution of hopping amplitudes, this opens up the study of monopole dynamics accounting for correlated statistics and also percolation effects which may play a prominent role in understanding also the so called “quantum” spin ices. The quantitative benefit of this theory is intimately related to neutron scattering in condensed matter.

B. Tomasello, C. Castelnovo, R. Moessner, J. Quintanilla,
Correlated quantum tunneling of monopoles in spin ice,
Phys. Rev. Lett. 123, 067204 (2019) (arXiv)