Aug 05, 2021
Research: Key to exact bosonization duality in two spatial dimensions
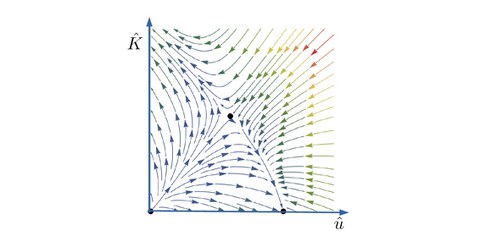
Figure caption: The renormalization group flow of the couplings in the theory. The existence of two nontrivial fixed points (corresponding to O(2) x O(2) and O(4) symmetries) allows us to conclude the existence of a critical point and, therefore, predict a continuous phase transition.
Many quantum phase transitions can be described via the Landau-Ginzburg-Wilson paradigm based on the notions of an order parameter and symmetry breaking. However, in the case of systems with competing order parameters, the predictions of the paradigm do not always agree with numerical results. The lack of consensus in the literature regarding the type of the phase transition in such systems motivated us to examine a specific type of two-dimensional quantum antiferromagnets with an anisotropy forcing the spins to lie in one plane. In our theory, we have additionally considered a non-trivial topology of the emergent gauge fields, which induce vortex loops in the system.
Our work has shown that two-dimensional topological anisotropic antiferromagnets undergo a continuous phase transition, which goes beyond the traditional theory of quantum phase transitions. The mechanism underlying such behavior is dubbed “deconfined quantum criticality” and refers to the fact that while antiferromagnetic and paramagnetic phases are described by two different order parameters both of those descriptions do not persist at the critical point but rather fall apart (deconfine) into more elementary fields. Besides demonstrating and explaining the existence of a continuous transition, we were able to make a few precise predictions about the near-critical behavior of the theory. The results can actually be tested experimentally in so-called chiral spin liquid systems and bilayer quantum Hall systems.
The topology of our theory was instrumental in obtaining the continuous transition and helped produce another beautiful result — an exact bosonization duality for massless Dirac fermions in two spatial dimensions. While for one-dimensional theories, the transmutation between bosons and fermions is well-established, everything becomes more complicated once we move one dimension higher. In two spatial dimensions, such derivations were only available for massive fermions, while the massless case had remained a conjecture. In our paper we managed to overcome this gap in theory and suggested bilayer quantum Hall ferromagnets as a platform to explore this duality experimentally. We hope soon there will be empirical evidence of the transmutation of bosons into fermions in two dimensions.
V. Shyta, J. van den Brink, F. S. Nogueira,
Deconfined Criticality and Bosonization Duality in Easy-Plane Chern-Simons Two-Dimensional Antiferromagnets,
Phys. Rev. Lett. 127, 045701 (2021) (arXiv)
