Research: Quantum Origin of Limit Cycles, Fixed Points, and Critical Slowing Down

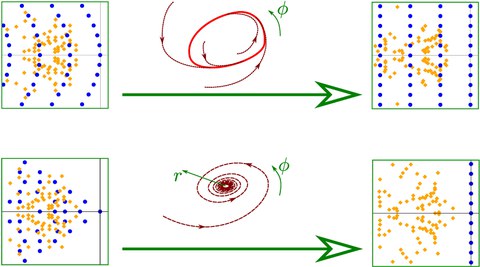
The question of how classical behavior appears as an appropriate limit of quantum dynamics has
intrigued physicists since the dawn of quantum mechanics.  Available insights into this question are predominantly for energy-conserving (Hamiltonian) systems.  However, most of the iconic nonlinear phenomena in classical systems, such as limit cycles, bifurcations, period doubling to chaos, are described by coupled differential equations that are dissipative. What is their quantum origin?   This work addresses the emergence of such behaviors from a quantum description, focusing on a Lindbladian description.  Signatures of limit cycles, Hopf bifurcations and fixed points are identified in the spectrum of the quantum Liouvillian.

S. Dutta, S. Zhang, M. Haque,
Quantum origin of limit cycles, fixed points, and critical slowing down,
Phys. Rev. Lett. 134, 050407 (2025) (arXiv)