Internships for school students

The course is aimed at school students who are aiming for a general higher education entrance qualification (Abitur).

Are you interested in abstract structures, symmetries and puzzles?

Selbstorganisation interagierender Partikel

Are you fascinated by interrelationships in nature and technology and want to know how these can be described using mathematical models and simulated using a computer?

"What does mathematics have to do with music and art?"

Would you like to know what holds the world together at its core?

Would you like to study STEM subjects?

Then you will certainly enjoy a student internship at the Faculty of Mathematics at TU Dresden. Our professors and staff offer various internships for high school students from the 9th grade onwards, e.g. as a company internship for career orientation.

General information

In our internships

you will get to know exciting mathematics as part of a small student project and gain an insight into current mathematical research,
you can find out about studying mathematics and get a taste of lectures,
you will get to know students and lecturers from the Faculty of Mathematics.

Topics. The thematic focus of our internships is diverse - from "pure" mathematics to mathematics at the interface with nature, technology, art and music. You can find a list of current internships here.

Duration. The internships are designed for 2 weeks.

Group. We prefer to carry out the internships in groups of up to 4 students. We put the groups together ourselves, but you can also register as a group with your classmates.

Registration and application

Please send your application via email to (recipient: Dr. Antje Noack, Prof. Stefan Neukamm)

Prerequisites

Curiosity and a high level of motivation
Interest in the topic of the project
Ability to work independently and in a team
Good to very good academic performance (i.e. grade point average better than 2.0), especially in mathematics

Application documents

Your application should include the following information in particular

Internship period
Name your preferred internship project and 2 alternative projects. You can refer to the short names in the list.
Letter of motivation: Why do you want to do an internship with us and why are you interested in the project.
Curriculum vitae in tabular form
Current certificate

Application procedure

The internships for the 2025/2026 school year will be awarded from October 2025. They will be awarded in stages, i.e. all applications up to October will be collected and awarded on November 1. They will then be awarded again on December 1 and January 1. For internships that take place in November, we will contact you beforehand. We will try to take your preferred projects into account when allocating them. However, it can also happen that we suggest a completely different project if the desired projects are already full or cannot be offered at the moment.

Internship projects

Our range of internship projects is currently being updated, i.e. some projects will be dropped and new ones will be added. This is expected to be finalized by mid-October at the start of the semester.
Applications for the school year 25/26 can already be submitted now. Please indicate all desired projects from the following list and send us an additional e-mail in October if anything changes.

P1 - Project "Mathematics, music and vibrating strings"

Head: Prof. Stefan Neukamm - Chair of Applied Analysis
Description: What do tones, sounds and noises look like and what do functions sound like? What do musical intervals, trigonometric functions and the physics of vibrating strings have to do with each other? How can we mathematically model a vibrating string and simulate it on the computer? In the practical course, we investigate these and other questions in the group using methods of analysis and with the help of simple simulations that we program ourselves in Python. You can find a final presentation on last year's project here.
Applicant profile: Interest in math and science. Helpful: You play an instrument.
Keywords: Analysis, mathematical modeling, programming with Python, musical intervals, overtone series, tuning systems
Max. Group size: 4

P2 - Project "Vectors and matrices"

Head: Dr. Antje Noack - Institute of Algebra
Description: Forces are visualized by vectors. A chessboard can be represented by a simple matrix. Vectors and matrices are used as aids in many other applications. We want to get to the bottom of this. You will familiarize yourself with the topic independently and become familiar with the properties of these objects through various exciting tasks. You will use the Matlab (or Python) software package to write small programs, for example to move polygons in the plane.
Applicant profile: Interest in mathematics and natural sciences.
Keywords: linear algebra, programming
Max. Group size: 4

P3 - Project "Modulo computation and cryptography"

Head: Dr. Julia Goedecke - Institute of Geometry
Description: Cryptography, i.e. the encryption of sensitive data or messages, is essential in many places in today's world: for example, for secure Internet communications (including WhatsApp), the protection of government or industrial secrets or sensitive customer data, and Internet shopping. After a brief introduction to the historical beginnings (e.g. Caesar encryption), this project deals with modular arithmetic and the RSA algorithm. This is an asymmetric encryption method, also known as the public-key method. Everyone who can read the clock has done modular arithmetic before, and you will learn the mathematical basics of it. You will work your way into the subject independently and can explore various aspects through exciting tasks, as well as getting to know a few small proofs. You may also do some programming with the MatLab software package.
Applicant profile: Interest in mathematics and/or computer science
Keywords: Cryptography and number theory
Available period: immediately
Max. Group size: 4

P4 - Project "Simulation of the kicked rotor - Nonlinear systems in physics "

Head: Lukas Keller - Institute of Numerical Mathematics
Description: The kicked rotor is a classical example of a nonlinear system that can exhibit chaotic motion. This phenomenon is often used in physics and mathematics as an example of complex behavior. In this lab, we will explore the basic physical principles behind the kicked rotor and simulate them in Python. We will investigate to what extent we can describe the complex behavior of this system with simple mathematical models and simulations and illuminate it under different conditions.
Objectives of the internship: Mathematical modeling of the kicked rotor; implementation and simulation of the system with Python; visualization and analysis of the results
Applicant profile: Interest in mathematics, physics and programming
Keywords: Nonlinear systems, simulation, Python, mechanics
Available period: immediately
Max. Group size: 3

P5 - Project "Head over heels into the minimum - Optimizing with Python"

Head: Prof. Alexandra Schwartz, Carolin Leili - Chair of Mathematical Optimization
Description: You've probably seen a cartoon in which someone tumbles down a slope and keeps rolling over ("ouch, ouch..."). This is exactly the idea - at least as a vivid image - behind a mathematical process that can be used to find the minimum points of functions. The exciting thing about it is that you only need math that you already know from school! In our internship, you will learn the basics of programming with Python and develop your own program step by step that solves such minimization tasks - from simple examples to a method that can even handle functions with several variables.
Applicant profile: Interest in mathematics and programming, a good spatial imagination is helpful
Keywords: optimization, programming with Python, notion of function, points in the plane
Max. Group size: 2

P6 - Project "Mathematics of pattern formation"

Head: JProf. Markus Schmidtchen - Chair of Applied Mathematics
Description: If you take a closer look, you will discover self-organization almost everywhere in nature. A very vivid example of self-organization are flocks of birds that form although there is no 'leader' that orders this behaviour. Similar behavior can also be observed in schools of fish or herds of animals. And what does mathematics have to do with this? In the practical course on pattern formation, we want to investigate together and use mathematical formalisms to model how self-organization and pattern formation can occur in large groups. We will then simulate the behavior on the computer.
Applicant profile: Interest in mathematics and the natural sciences
Keywords: mathematical modelling, self-organization, dynamics of large groups
Max. Group size: 4

P7 - Project "3 panel projections"

Head: Prof. Manuel Bodirsky, Dr. Philipp Grzywaczyk - Chair of Algebra and Discrete Structures
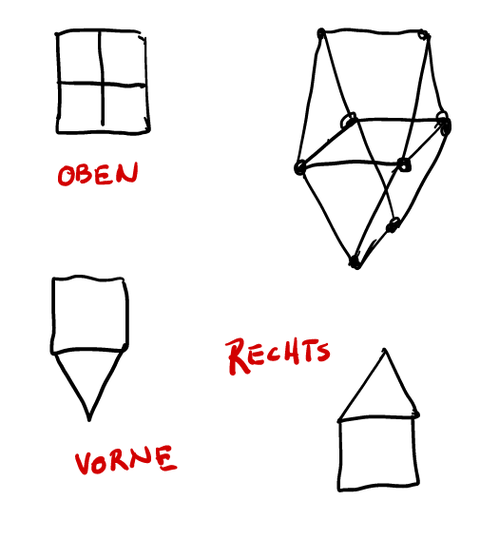
Description: In technical drawing, 3-panel projections (also known as "third angle projection" or "multiview orthographic projection") are used to represent three-dimensional constructions with the help of
two-dimensional projections (the panels). Typically, projections are chosen in three orthogonal directions in pairs; an example of this can be found in the figure on the right.
The question here is under which conditions the original construction can be recovered from given tables. Furthermore, we are interested in criteria to determine whether there is a construction with the corresponding panels for given panels at all. Even if we assume that the construction we are looking for is a polytope (as in the figure), there is still no known efficient algorithm that can decide for three given panels whether there is a construction that matches the given panels; this is therefore still an open research problem.

The aim of the project is to compile as comprehensive a catalog as possible of interesting examples of instances of this problem together with their solutions.
Each example should consist of

the 3 panels, i.e. the 3 projections from the 3 perspectives, and
a polytope that fits the three tables, or an argument that no such polytope can exist.

Applicant profile: Spatial imagination. Knowledge of linear algebra and discrete geometry is desirable, but not required.
Max. Group size: 4

P8 - Project "Discoveries with thread graphics"

Head: Heino Hellwig, LfbA Didactics of Mathematics, Institute of Analysis

Description: Simple thread diagrams offer a very attractive approach to Schmieggeraden and envelope curves (Enveloppe). They allow an experimental investigation of a variety of curves. Geogebra or Python (Turtel graphics) can be used to create elegant thread graphics. This creates patterns that require explanation and insight into their origin. Assumptions are made and evidence is provided. An outlook on the field of modeling with cubic Bézier curves could end the internship.
Applicant profile: Interest in mathematics and natural sciences.
Keywords: geometry, analysis, programming with Python
Max. Group size: 4

P9 - Project "Selected topics in one subject area"

Head: Faculty of Mathematics
Description: Have you already been intensively involved in an area of mathematics - perhaps through a subject paper, competitions such as the Mathematical Olympiad or simply out of personal interest? In this project, we offer you the opportunity to work individually on an advanced topic in mathematics. We will agree on the specific topic with you - based on your previous knowledge, interests and goals, which you should describe in as much detail as possible in your application.
Applicant profile: You have an above-average enthusiasm for mathematics and have already dealt with mathematical issues beyond the school curriculum.
Keywords: specialization in mathematics
Max. Group size: 1

Contact persons at the Faculty of Mathematics

Dr. Antje Noack, Tel.: 463 32149
Prof. Dr. Stefan Neukamm, Tel.: 463 33998
Contact:

You can find a complete overview of internships at TU Dresden for students here.