May 03, 2023
Research: Universal scaling of Klein bottle entropy near conformal critical points
Phase transitions are among the most intriguing phenomena in physics. When physical systems undergo a continuous phase transition, they exhibit universal scaling behaviors that are independent of microscopic details.
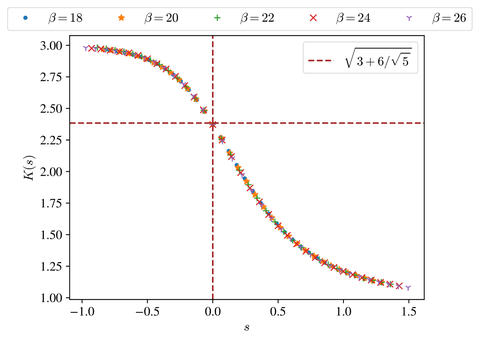
Conformal field theory is a powerful theoretical tool for studying phase transitions and critical phenomena in two-dimensional classical systems and one-dimensional quantum systems. For these systems, the conformal symmetry imposes strict constraints on the universal properties of physical observables. Thus, for a target microscopic model at criticality, it is important to identify which conformal field theory emerges in the low-energy, long-wavelength limit. One measure that has proven useful for this purpose is the Klein bottle entropy [Hong-Hao Tu, Phys. Rev. Lett. 119, 261603 (2017)], which is universal at conformal critical points, and its universal value provides a hint about the type of conformal field theory.
In a recent work, the scope of the Klein bottle entropy has been further extended to the off-critical region. By considering conformal field theory perturbed by a relevant operator, it is demonstrated that the Klein bottle entropy is a universal scaling function of the dimensionless coupling. This discovery allows the scaling dimension of the perturbation operator to be extracted via data collapse, providing additional valuable insight into the type of conformal field theory. Numerical calculations on several paradigmatic models indeed confirm the universal scaling of the Klein bottle entropy. This research opens a new avenue: near-critical systems placed on a non-orientable manifold may display novel features that could be valuable for identifying the nature of criticality.
Y. Zhang, A. Hulsch, H.-C. Zhang, W. Tang, L. Wang, H.-H. Tu,
Universal scaling of Klein bottle entropy near conformal critical points,
Phys. Rev. Lett. 130, 151602 (2023) (arXiv)