Modeling and Solving of Railway Optimization Problems
Motivation
A competitive rail transport within a single European transport zone is one of the key objectives of the European Union, both for freight and passenger transportation (Generaldirektion Mobilität und Verkehr 2016). In Germany, a steady increase in passenger transport performance can been observed for years, see Figure 1.
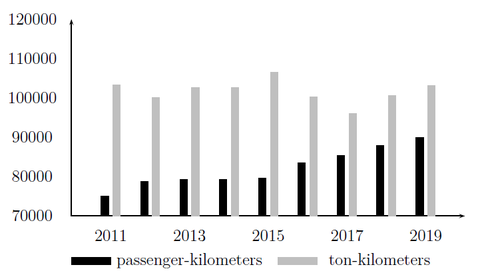
Figure 1: Transport performance in Millions
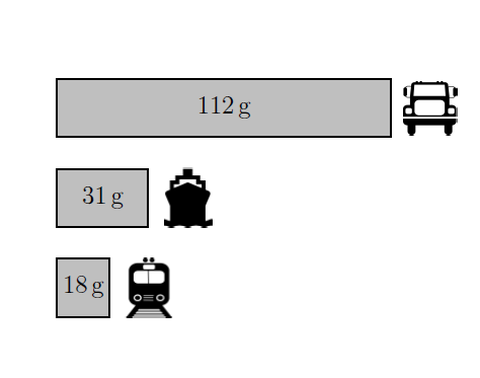
Figure 2: Greenhouse gas emissions per ton-kilometers
Here it is necessary to further increase the transport performance with limited resources and thus to apply a cost-efficient planning in order to remain competitive with other modes of transport. This applies especially for freight transport, where a stagnation can be observed, although the road freight transport performance has been rising continuously since 1995. Again, similar observations can also be made for whole Europe (Generaldirektion Mobilität und Verkehr 2019). This makes it very difficult to achieve both domestic German and pan-European environmental targets, especially due to the significantly poorer performance of road transport compared to rail transport in terms of greenhouse gas emissions, see Figure 2. Therefore, in addition to the urgently required political initiatives (BMVI 2017), cost-efficient planning for competitive market participation of the rail freight sector is of crucial importance. Regarding the share of different costs in the total expenditure of railway companies, both vehicle-based and personnel costs are particularly important. Figure 3 shows as an example the shares based on the profit and loss account of DB Regio AG for 2019.
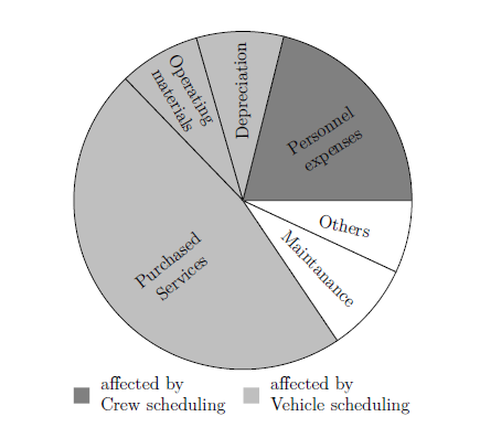
Figure 3: Share of expenses in the annual report of DB Regio AG 2019
About 80% of the purchased services are related to the use of infrastructure (i.e., renting tracks and stations). Over 90% of the operating materials are costs for energy (fuel and electricity). Nearly 94% of depreciation is related to vehicles. Over 80% of the personnel costs are incurred in the transport sector. Similar information can also be found for other European rail operators for both freight and passenger transport (SNCF Group 2020; BLS AG 2017). Figure 3 highlights the influence of two optimization problems on a majority of the expenses. Crew scheduling has a significant impact on the personnel costs of moving operations, as it can significantly affect the efficiency of the single duties as well as the total number of duties required and thus the number of employees. On the other hand, the influences of engine scheduling on the expenses are more diverse. Firstly, efficient vehicle usage makes it possible, for example, to save on empty runs and thus energy costs. This also leads to savings in infrastructure costs, as network usage can be reduced. Finally, the efficient use of vehicles also makes it possible to reduce their number, which would result in lower depreciation in the long term. Due to the influence of these two problems on central cost factors, efficient methods of solving them are of decisive importance in order to maintain or further increase the competitiveness of rail transport. Both planning problems raise considerable challenges to automated planning, as well in terms of their mathematical complexity as in terms of the large number of practical requirements. Therefore, suitable models have to be developed in combination with the implementation of efficient solution algorithms based on methods of operations research. This applies to freight as well as to passenger transport, whereby similar solution methods can be applied in each case.
Rolling Stock Scheduling is one of the most important planning tasks in both passenger and freight transportation because of the high share of costs (see Figure 3). In general, rolling stock scheduling deals with the planning of circulations for powered and unpowered vehicles. In passenger transport usually locomotives and cars are planned together or in close coordination. In freight transport the goal is to assign locomotives to trains. Since this work focuses on the problem in freight transport, only a presentation of this application area is given in the following. A brief literature review can be found in Scheffler /Neufeld /Holscher (2020) and a very detailed one is presented by Piu / Speranza (2014). Assigning locomotives to trains is called the Locomotive Assignment Problem (LAP), which is also known as Locomotive or Engine Scheduling Problem. Based on a preplanned train schedule, a set of locomotives have to be assigned to each train. A train is the smallest planning unit and defined by departure time and station, arrival time and station as well as operating requirements for the locomotives. Simultaneously, permissible circulations must be planned for the locomotives. For both, the assignment of locomotives to trains as well as for the generation of circulations a variety of requirements has to be considered. Especially combining two or more locomotives for moving a train results in considerable challenges during planning.
Crew Scheduling considers as major planning step the second movable resource: the personnel. It is one of the most challenging problems because of the huge amount of legal regulations, operating conditions and requirements from the transportation contract. On the one hand, the train drivers have to be scheduled for both passenger and freight transportation. On the other hand, conductors have to be scheduled additionally in passenger transportation. This work focuses on the latter in context of crew scheduling. A brief literature review is given in Neufeld et al. (n.d.) and a comprehensive one is presented by Heil /Hoffmann /Buscher (2020). In general, crew scheduling aims at creating a set of (anonymous) duties for covering a given set of trips. A trip is defined by departure time and station as well as arrival time and station. In the special case of conductors, however, some transportation contracts do not require the attendance of all trips, but require a percentage coverage. These so-called attendance rates are based on the distance (i.e., kilometers) and describe the ratio between attended and total (attended + unattended) kilometers of the network (crew scheduling problem with attendance rates, CSPAR). It is common that there are several (different) attendance rates for parts of the network or certain times of the day. It is also possible that more than one conductor is required (i.e., rates >100%). All rates that are not multiples of 100% represent an additional degree of freedom for the planning problem. Besides the decision which trip is attended by which duty, it is also necessary to decide which trips should be attended at all.
Purpose
The main aim of this work is to provide decision makers suitable approaches for solving two crucial planning problems in the railway industry. On the one hand, the focus is on practical usability and the necessary integration and consideration of real-life requirements in the planning process. On the other hand, solution approaches are to be developed, which can provide solutions of sufficiently good quality within a reasonable time by taking all these requirements into account. With regard to the LAP, mathematical problem formulations used in North America will first be adapted for application for a European freight operator. Additional requirements, which are characteristic for Europe, are integrated. Although solution approaches in the literature provide promising results, adaptations and improvements are necessary to solve European instances. Further a generalization of two different formulations is aspired. Crew scheduling with attendance rates is a rather less studied problem. Since the existing approaches are only suitable for smaller instance sizes, further development is essential. Again, this improvement is combined with the further integration of additional requirements, which are inevitable for practical application. In addition to cost-oriented crew scheduling, one upstream and one downstream issue for which no automated planning approaches exist so far are discussed and analyzed. Besides the planning perspective of the railroad operator, the general cost effects resulting from demanding attendance rates in the transportation contract are examined. The purpose of this work can be summarized in the following research questions:
Q1 How can the iterative heuristic of Ahuja et al. (2005) be accelerated for solving European instances of the locomotive assignment problem?
Q2 How does the reasonable restriction of the solution space allow an accelerated solution of the locomotive assignment problem?
Q3 How can real-world instances of railway crew scheduling problems with attendance rates be solved for practical application?
Q4 What cost effects result from the use of attendance rates?
Q5 How can the daily distribution of duties during solving crew scheduling problems with attendance rates be controlled?
Q6 How can suitable locations for crew bases of conductors be determined?
| Contact: | Martin Scheffler |
| Duration: | since November 2017 |
