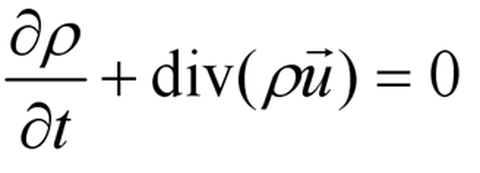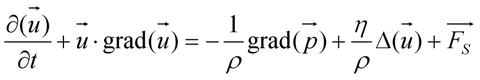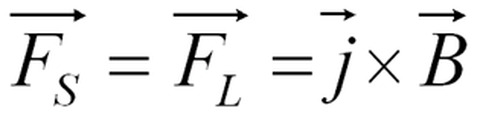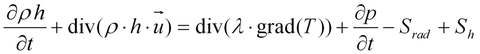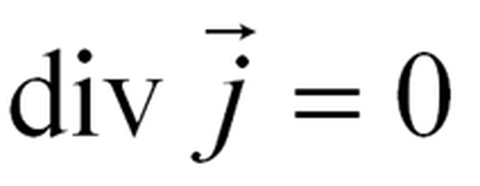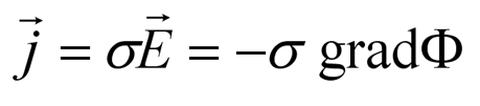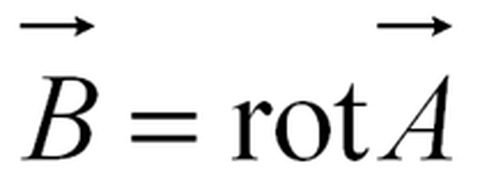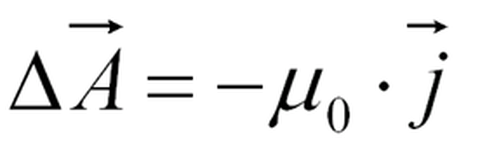Simulation
Die numerische Simulation ermöglicht die schnelle und räumlich hoch aufgelöste Beschreibung von komplexen physikalischen Prozessen. Die entwickelten Modelle stehen zur Berechnung von WIG-, Plasma- oder MSG-Prozessen zur Verfügung. Weiterhin können Aussagen über die Schutzgasströmung, die Temperaturverteilung im Brenner, den Werkstoffübergang oder die Schmelzbadströmung getroffen werden.
Ein Lichtbogen ist eine sich selbst erhaltende elektrische Gasentladung. Infolge eines ausreichend großen elektrischen Potentials zwischen Anode und Kathode fließt in einem thermisch ionisierten Gas (Plasma) ein elektrischer Strom. Die hohe elektrische Stromdichte erhält durch die Widerstandserwärmung die für die Leitfähigkeit notwendige Temperatur des Lichtbogens aufrecht. Die Begrenzung des leitfähigen Querschnitts des Lichtbogens stabilisiert die Gasentladung.
Die Physik der Bogensäule kann durch das magneto-hydro-dynamische Modell (MHD) eines elektrisch leitfähigen Fluids abgebildet werden. Dieses Modell beschreibt die sich gegenseitig beeinflussenden elektromagnetischen und fluiddynamischen Prozesse in elektrisch leitenden Flüssigkeiten.
Die Grundgleichungen der Fluiddynamik sind die Navier-Stokes-Gleichungen. Sie verkörpern ein System von nichtlinearen partiellen Differentialgleichungen 2. Ordnung, bestehend aus dem Masseerhaltungssatz, dem Impulserhaltungssatz und dem Energieerhaltungssatz.
Aus dem Masseerhaltungssatz wird die Kontinuitätsgleichung für kompressible Fluide abgeleitet:
Aus dem Zweiten Newtonschen Axiom ist der Impulserhaltungssatz abzuleiten. Die zeitliche Änderung des Impulses ist gleich der Summe der am Volumenelement wirkenden Kräfte.
Im kartesischen Koordinatensystem ergeben sich drei voneinander unabhängige Gleichungen. Die Terme auf der rechten Seite der Gleichung repräsentieren von links nach rechts die Druckkraft infolge der Druckgradienten, die Reibungskraft infolge von Schub- und Scherkräften im Medium und die so genannten Volumenkräften wie z. B. die Gravitations-, die Zentrifugal- und die Corioliskraft. Durch das MHD Modell wird die Lorentzkraft implementiert.
Die Enthalpiegleichung resultiert aus dem Ersten Hauptsatz der Thermodynamik. In einem offenen System und für langsam strömende Fluide ist die Summe der über die Grenzen transportierten Energie gleich der Energieänderung innerhalb des Kontrollvolumens.
Es werden an dieser Stelle auch die Nettostrahlungsemission und die Widerstandserwärmung berücksichtigt. Die Grundgleichungen der Elektromagnetik sind die Maxwellgleichungen. Im MHD Modell werden diese zum Berechnen der elektrischen Stromdichte und des Magnetfeldes genutzt. Für eine stationäre Entladung gilt unter Berücksichtigung der Quasineutralität:
Die Stromdichte folgt aus dem verallgemeinerten Ohmschen Gesetz. Die induzierten Feldstärken und das Hallfeld sind gegenüber der Feldstärke im Lichtbogen zu vernachlässigen.
Es folgt:
Die magnetische Flussdichte (umgangssprachlich als Magnetfeld bezeichnet) wird unter Verwendung des Vektorpotentiales berechnet.
Prinzipiell ist es möglich, durch die Vernachlässigung beziehungsweise starke Vereinfachung der Fallgebiets-mechanismen den Lichtbogen mit Hilfe der genannten Gleichungen zu berechnen. Es wurden im Rahmen der Projekte aber auch Modelle erarbeitet, die komplexe Fallgebietsmechanismen oder Entmischungseffekte berücksichtigen.
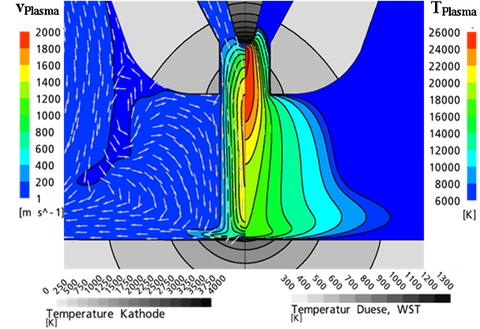
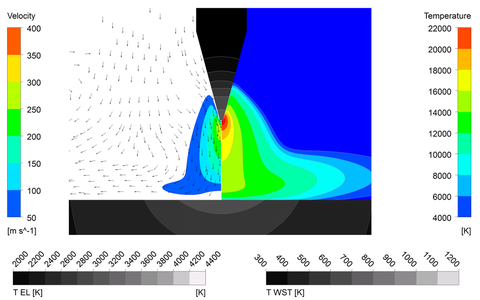
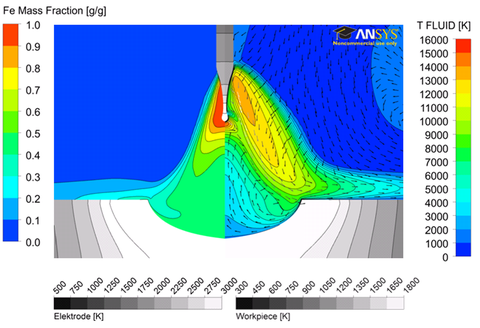
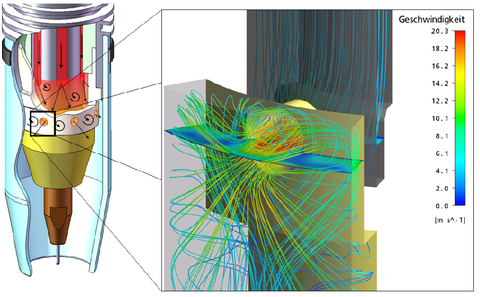
Beispiele verschiedener visualisierter Simulationsergebnisse:
Darstellung des Geschwindigkeitsfeldes und der Sauerstoffkonzentration der Schutzgasströmung eines MSG-Schweißbrenners © TU Dresden
Darstellung des Geschwindigkeitsfeldes und der Sauerstoffkonzentration der Schutzgasströmung eines MSG-Schweißbrenners während eines Impulslichtbogen Prozesses © TU Dresden