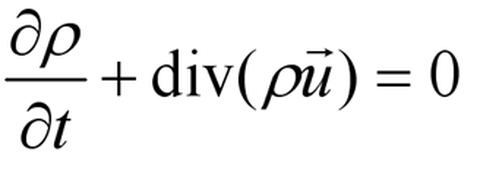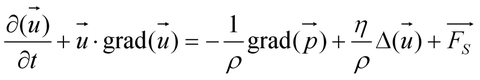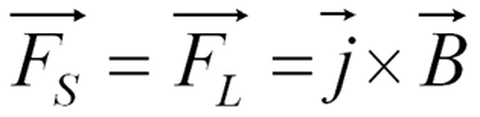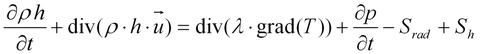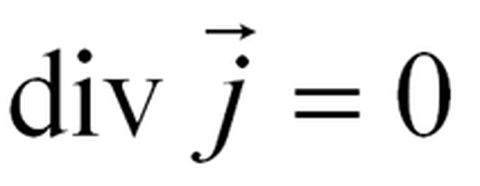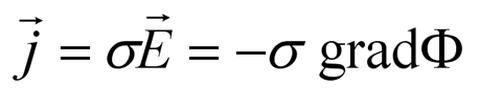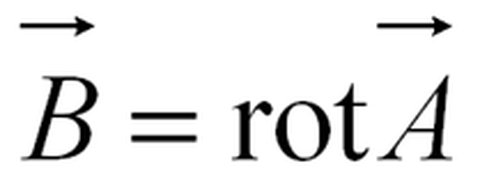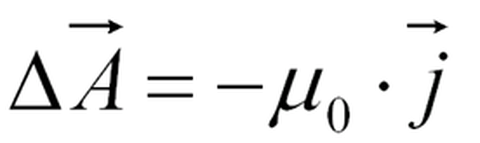Simulation
The numerical simulation enables a fast and spatially high-resolution description of complex physical processes. The resulting models can be used to calculate TIG, plasma or gas metal arc welding (GMAW) processes. Assertions can also be made regarding shielding gas flow, torch temperature distribution, material transition or weld pool flow.
An electric arc is a self-sustaining electrical gas discharge. Following sufficiently great electrical potential between anode and cathode, an electrical current passes through a thermally ionized gas (plasma). Due to the heat generated from electrical resistance, the high current density maintains the temperature needed for the arc to conduct electricity. Restricting the conductive cross-section of the arc stabilizes the gas discharge.
The physics of the arc column can be demonstrated by the magnetohydrodynamics model (MHD) of electrically conducting fluids. This model describes the electromagnetic and fluid dynamic processes in electrically conducting fluids that interact with each other.
The Navier-Stokes equations form the core equations for fluid dynamics. They embody a system of 2nd order nonlinear partial differential equations comprising the laws of conservation of mass, conservation of momentum and conservation of energy.
The continuity equation for compressible fluids is derived from the law of conservation of mass:
The law of conservation of momentum is based on Newton's second second law of motion. The change in momentum over time is equal to the sum of the forces acting on the volume element.
Three independent equations arise from the Cartesian coordinate system. The terms on the right side of the equation represent, from left to right, compressive force due to pressure gradients, friction due to shearing forces in the medium, and body forces such as gravitational, centrifugal, and Coriolis forces. The Lorentz force is implemented by the MHD model.
The enthalpy equation comes from the first law of thermodynamics. In an open system and for slowly flowing fluids, the sum of the energy transported across the boundaries is equal to the change in energy within the control volume.
Net radiant emission and resistance-generated heat are also taken into account at this point. Maxwell’s equations are the core equations of electromagnetism. These are used in the MHD model for calculating the electrical current density and the magnetic field. For a steady-state discharge, taking quasi-neutrality into account, the following applies:
The current density is determined by applying a generalization of Ohm's law. The induced field strengths and the Hall effect are negligible compared to the field strength in the arc.
Thus:
The magnetic flux density (also known as the magnetic field) is calculated using the vector potential.
In principle, it is possible to calculate the arc using the above equations by neglecting or greatly simplifying the drop zone mechanisms. However, these projects have also developed models that take complex drop zone mechanisms or phase separation effects into account.
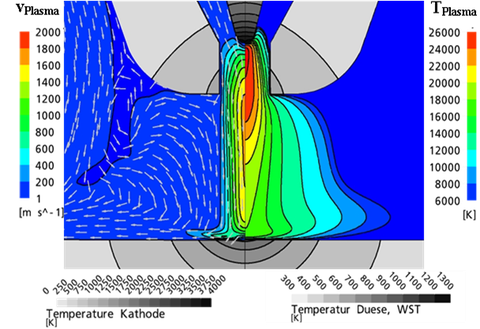
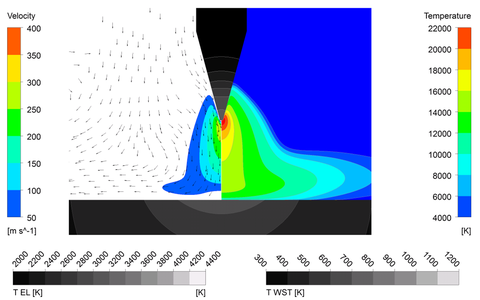
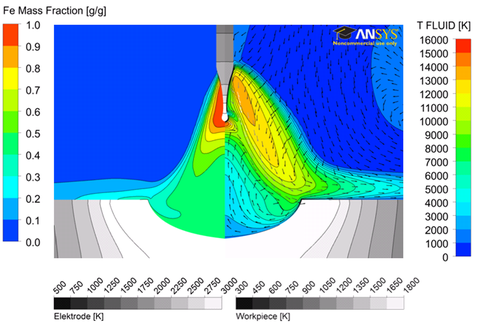
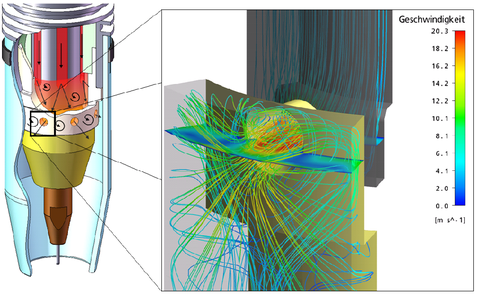
Examples of various visual simulation results:
Darstellung des Geschwindigkeitsfeldes und der Sauerstoffkonzentration der Schutzgasströmung eines MSG-Schweißbrenners © TU Dresden
Darstellung des Geschwindigkeitsfeldes und der Sauerstoffkonzentration der Schutzgasströmung eines MSG-Schweißbrenners während eines Impulslichtbogen Prozesses © TU Dresden