Flow of complex fluids
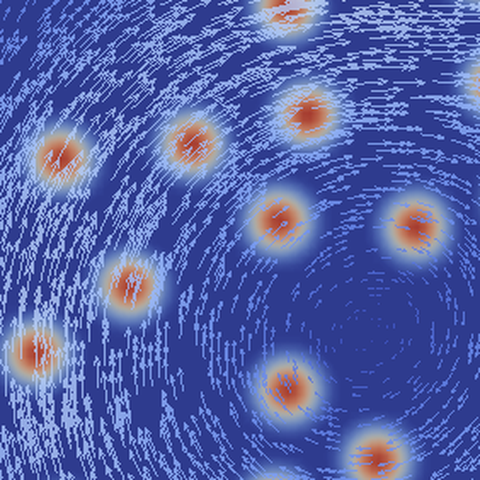
Colloidal particles immersed in a fluid interacting with the fluid and with each other.
Particles, droplets or cells immersed in a fluid change the flow behavior due to hydrodynamic interactions of the objects. In the simplest case, the fluid-structure interaction can be modeled with non-deformable (spherical) objects that induce an effective stress in the fluid. In a setup driven by gradient flow, a corresponding stress tensor or volume force can be derived from thermodynamic considerations.
Particulate Flow
We have studied a phase-field crystal model to describe the spherical particles and a Navier-Stokes equation to describe the flow field. A combination of both leads to a simple fluid-structure interaction model for (soft) spherical particles. One question we tried to answer is where and how the particles disturb the dynamical behavior of the fluid, i.e. can dynamic barriers be broken by particles of non-zero size, such as the line barrier in a double-gyre flow.
Multiphase flow in porouse media
In the printing process, a quantity of liquid is applied to the surface of a sheet of paper. The water-based solution is intended to be absorbed by the microscopic structure of the paper. Liquid penetration is mainly driven by capillary forces resulting from the interplay between surface tension and a wetting angle. These forces can be controlled by varying the different coating layers on a fiber network that forms the core of the paper.
To simulate this process, a two-phase flow problem was formulated and implemented using a diffuse-interface method and finite-element discretization. The microscopic granular structure of the coating layers was resolved by a fine mesh. In order to adapt the geometric structure to realistic materials, a semi-automatic mesh generator was implemented, which allows to control the granularity parameters and the structure of the capillary network. The latter is responsible for the penetration velocity and the absorption time, which are of fundamental interest to industrial partners.
Student projects and thesis topics
- Master thesis: "Collective Behaviour of Active Brownian Particles
by Active VPFC Modeling" (S. Yaskovets, 2022) - Incorporating an interaction strategy for the particles based on their local shap orientation
Publications
- M. Residori, S. Praetorius, P. de Anna, and A. Voigt, The influence of finite size particles on fluid velocity and transport though porous media, Physical Review Fluids, Juni 2023, (accepted) [arXiv]
- S. Praetorius and A. Voigt, Fluid penetration in Paper Structures, In German Success Stories in Industrial Mathematics (submitted), 2017. [bibtex]
- S. Ling, W. Marth, S. Praetorius, and A. Voigt, An adaptive finite element multi-mesh approach for interacting deformable objects in flow, In Comput. Meth. Appl. Math., Vol. 16, pp. 475–484, 2016. [doi] [bibtex]
- S. Praetorius and A. Voigt, A Navier-Stokes phase-field crystal model for colloidal suspensions, In J. Chem. Phys., Vol. 142 (15), pp. 154904, 2015. [doi] [bibtex]
- S. Praetorius and A. Voigt, A Phase Field Crystal Approach for Particles in a Flowing Solvent, In Macromol. Theor. Sim., Vol. 20 (7), pp. 541–547, 2011. [doi] [bibtex]
