Software Development of Finite-Element Code
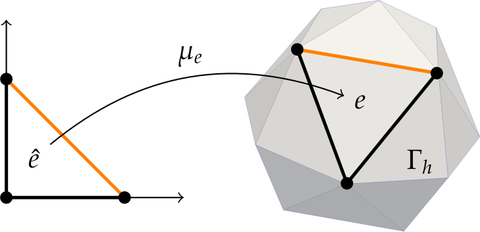
Parametrization of geometric grid elements
This project focuses on the development of the finite element framework AMDiS - Adaptive Multi-Dimensional Simulations. This numerical software was created at the Institute for Scientific Computing at the Technische Universität Dresden in 2005 and has been developed in several directions since then. This includes a domain-specific embedded language to formulate (bi-)linear forms using C++ expression template techniques. Numerical techniques are developed with and in AMDiS, such as the multi-mesh approach and an equation-based parallelization with local information exchange for the simulation of the coupling of 1000's of Cahn-Hilliard-like evolution equations.
Since 2017, the AMDiS framework is based on the Dune - the Distributed Unified Numerics Environment. This collection of numerical software modules is developed by several scientific computing and numerics groups at different German universities, but also has contributors from all over the world.
The AMDiS and Dune software is the basis for many research projects, but can also be used for teaching the finite element method and other grid-based discretization methods.
Student projects and thesis topics
- Masterarbeit: "Periodic Boundary Conditions on periodic and non-periodic Meshes: Methods, Implementation, Examples and Analysis" (F. Unruh, 2023)
- Masterarbeit: "Code Generation for Finite Element Simulation: Interfacing AMDiS from Python" (J. Drechsel, 2024)
- Masterarbeit: "Overlapping Domain Decomposition Methods for the Efficient Solution of Partial Differential Equations" (W. Jeon, 2024)
- Local assembling of Dirichlet-type boundary conditions.
- Incorporation of blocked and hierarchic data structures from Dune-istl and PETSc.
- Expression templates with symbolic differentiation for operators in (bi-)linear forms.
Associated software projects
- AMDiS, AMDiS (old implementation)
- Dune and various Dune modules, e.g., Dune-curvedgrid, Dune-curvedgeometry, Dune-vtk, Dune-gmsh4
Publications
- C. Engwer, C. Gräser, S. Müthing, S. Praetorius, and O. Sander. Concepts for Composing Finite Element Function Space Bases. 2025, [arxiv]
- M. Blatt, S. Burbulla, A. Burchardt, A. Dedner, C. Engwer, C. Gräser, C. Grüninger, R. Klöfkorn, T. Koch, S. Ospina De Los Ríos, S. Praetorius, and O. Sander. The Distributed and Unified Numerics Environment (DUNE), Version 2.10. 2025, [arxiv]
- S. Praetorius and F. Stenger. Dune-curvedgrid - a dune module for surface parametrization. Arch. Numer. Soft. 6:1, February 2022, [doi] [arxiv]
- S. Praetorius and A. Voigt. Collective cell behavior - a cell-based parallelization approach for a phase field active polar gel model. Proceedings of the 9th NIC Symposium, 49:369-376, February 2018. [url]
- S. Ling, W. Marth, S. Praetorius, and A. Voigt. An adaptive finite element multi-mesh approach for interacting deformable objects in flow. Comput. Methods Appl. Math. 16:475-484, January 2016. [doi]
- T. Witkowski, S. Ling, S. Praetorius, and A. Voigt. Software concepts and numerical algorithms for a scalable adaptive parallel finite element method. Adv. Comput. Math., pages 1-33, January 2015. [doi]
