Liquid Crystals on curved manifolds
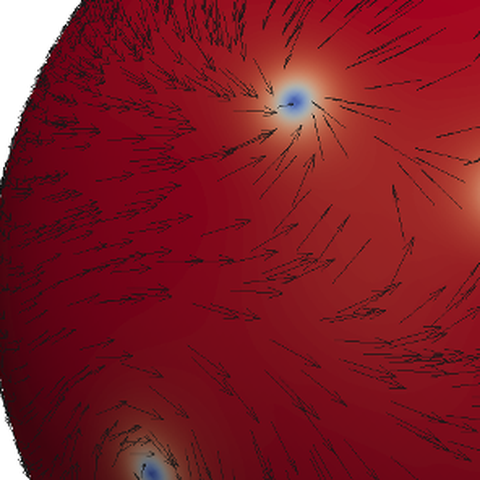
Defects in a polar liquid crystal film on a sphere. Colors indicate a polar order.
Liquid crystals are composed of anisometric molecules, such as rods or plates, and have an order of orientation and translation. They can be characterized in one sense as a liquid and in another as a solid. Forcing the molecules to locate at a liquid-liquid interface and to orient themselves tangentially to that surface results in interesting crystal arrangements.
Research focus
We study three types of models: First, a discrete particle model where form and interaction are explicitly given. Second, a continuous field-theoretic model for orientational order, and third, a combination of translational and orientational order. The first model is analyzed in collaboration with Francesco Alaimo, the second with Michael Nestler and Ingo Nitschke, and the third is a joint research topic with Hartmut Löwen and Raphael Wittkowski from Düsseldorf and Münster, respectively.
Student projects and thesis topics
- Phase-Field Crystal Q-tensor model restricted to surfaces using a projected FEM approach
- Implementing PFC and polar order in a DEC discretization
- Tensor-spherical-harmonics for Q-tensor equations
Publications
- I. Nitschke, M. Nestler, S. Praetorius, H. Löwen, and A. Voigt, Nematic liquid crystals on curved surfaces — a thin film limit, (submitted), 2017. [bibtex]
- M. Nestler, I. Nitschke, S. Praetorius, and A. Voigt, Orientational order on surfaces - the coupling of topology, geometry, and dynamics, In J. Nonlinear Sci., 2017. [doi] [bibtex]
- S. Tang, S. Praetorius, R. Backofen, A. Voigt, Y.-M. Yu, and J. Wang, Two-dimensional liquid crystalline growth within a phase-field-crystal model, In Phys. Rev. E, Vol. 92, pp. 012504, 2015. [doi] [bibtex]
- S. Praetorius, A. Voigt, R. Wittkowski, and H. Löwen, Structure and dynamics of interfaces between two coexisting liquid-crystalline phases, In Phys. Rev. E, Vol. 87, pp. 052406, 2013. [doi] [bibtex]
- R. Backofen, M. Gräf, D. Potts, S. Praetorius, A. Voigt, and T. Witkowski, A Continuous Approach to Discrete Ordering on S2, In Multiscale Model. Sim., Vol. 9 (1), pp. 314–334, 2011. [doi] [bibtex]
