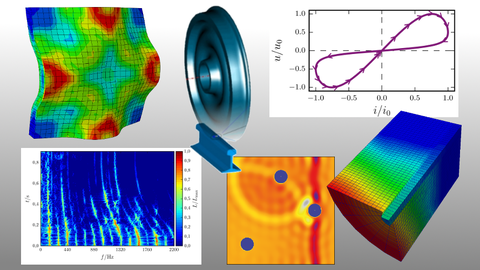
Research Field "Dynamics of Continua"
Engineering structures are often exposed to dynamic loads. In this research field both numerical and analytical methods are developed and help to adequately model the nonlinear dynamic behaviour of these structures made of heterogeneous materials. This also allows for a resource efficient dimensioning.
Research Projects
Cooperation with:
Prof. Dr.-Ing. habil. Daniel Balzani (Ruhr-Universität Bochum)
Abstract:
Predamaged structures made of fiber reinforced composites may withstand dynamical loads due to the crack bridging of the fibrous reinforcement. However, these fibers may be pulled out of the surrounding matrix material if the dynamic loads exceed critical measures. This research project deals whith the description of the phenomena associated with fiber pullout. Special emphasis is on the successive failure of the bond between the fiber and the surrounding matrix, which is due to the (tensile) wave propagation along the fiber axis, and on the leakage of the wave within the fiber into the matrix. The investigations are performed for composites consisting of modern reinforcement materials and a brittle matrix.
References:
"Analytical and Numerical Modelling of a Sub- and Supersonic Moving Load Front Along a Rod’s Skin", W. E. Weber, Y. F. Fangye, D. Balzani, B. W. Zastrau, Kapitel 26 in "Advanced Methods of Continuum Mechanics for Materials and Structures", Eds.: K. Naumenko and M. Aßmus; 2016, DOI: 10.1007/978-981-10-0959-4_26
"On the Mechanical Modeling and Analysis of the Dynamical Fiber Pullout Mechanism Taking into Account the Damage and Viscoelasticity of the Bond", Dissertation Aussama Azzam, M.Sc., 2015
Cooperation with:
Prof. Dr.-Ing. habil. Daniel Balzani (Ruhr-Universität Bochum)
Abstract:
Impact loads lead to severe stresses in structures made of fiber reinforced concrete. In order to secure humans, other animate beings and goods, these structures should have a high impact resistance. This research project especially deals with the modelling of the phenomena occurring in both the inhomogeneous material and the structure related to impact loads. Thus, the modelling takes place from the micro- to the macro-scale. Special emphasis is on the wave propagation, damping, and anisotropic damage including bond degradation. Another topic of interest is the construction of representative volume elements.
References:
"Analytical and Numerical Modelling of a Sub- and Supersonic Moving Load Front Along a Rod’s Skin", W. E. Weber, Y. F. Fangye, D. Balzani, B. W. Zastrau, Kapitel 26 in "Advanced Methods of Continuum Mechanics for Materials and Structures", Eds.: K. Naumenko and M. Aßmus; 2016, DOI: 10.1007/978-981-10-0959-4_26
BALZANI, Daniel; BRANDS, Dominik; SCHRÖDER, Jörg. Construction of statistically similar representative volume elements. In: Plasticity and Beyond. Springer Vienna, 2014. S. 355-412.
"ANALYTICAL DESCRIPTION OF FRC SUBJECTED TO TRANSIENT LOADS“, W. Weber, B. W. Zastrau, erschienen in "Journal of Theoretical and Applied Mechanics", Vol. 51, No. 1, S. 183-194; 2013
Cooperation with:
Prof. Dr.-Ing. habil. Daniel Balzani (Ruhr-Universität Bochum)
Abstract:
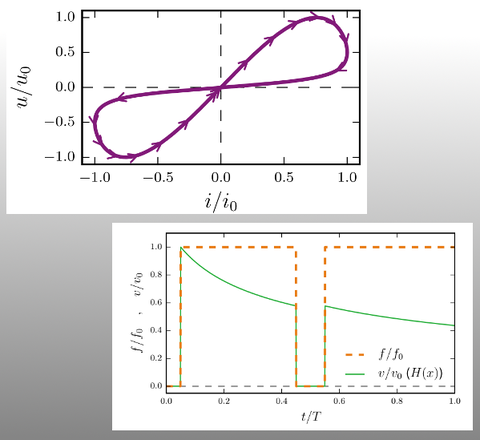
This project deals with the dynamic behaviour of materials with memristive properties. Here, the term memristance is adopted from electrical engineering. It describes the behaviour of the so called memristor, a nonlinear resistor with memory effect. Transferred to engineering mechanics, such a behaviour corresponds to a material with nonlinear, history-dependent damping properties. The object of investigation are effective numerical methods which enable calculations of structures with memristive material properties.
References:
Haas, L., Untersuchung elektro-mechanischer Analogien unter besonderer Berücksichtigung von Memristoren (Investigation of electro-mechanical analogies with particular consideration of memristors), Bachelorarbeit. Institut für Mechanik und Flächentragwerke, Technische Universität Dresden, Dresden, 2015
<2 more ref's, in print>
Abstract:
Within this project, problems of continuum mechanics with non-material boundary conditions are investigated. Boundary conditions are classified as non-material if they are assigned to different material particles over time. The extension of the classical field-equations of continuum mechanics by such boundary conditions is realized by application of Arbitrary-Lagrange-Euler-Kinematics. Therefore a notation, which assigns the particular placement to field quantities and operators, is developed. The advantages of this notation can be identified particularly with regard to a consistent representation of derivative operators. Conclusions on the transformation of the equations of motion of three-dimensional continua are derived from the determined (semi-)analytical solutions. For this reason the developed methods are usable in many technical applications. The vibration analysis of axially moving paper sheets, lift ropes, rollers as well as space tethers can be stated as an economical important example.
Franze, A. & Zastrau, B. W.: Analytical solutions for the one-dimensional wave equation with non-material boundary conditions, In: Selected dynamical problems in mechanical systems - theory and applications in transport, Warschau, 2014
Abstract:
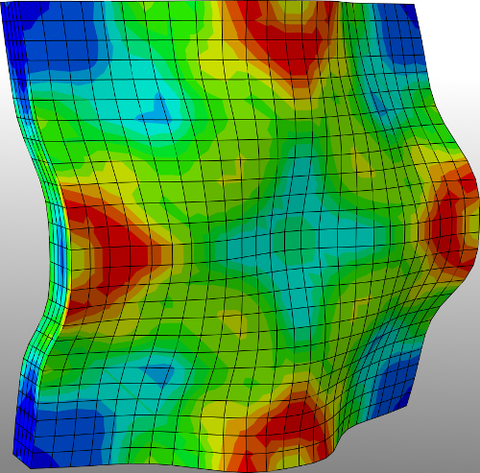
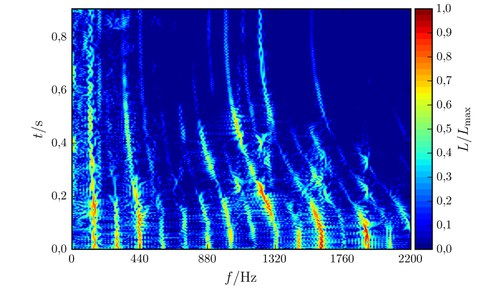
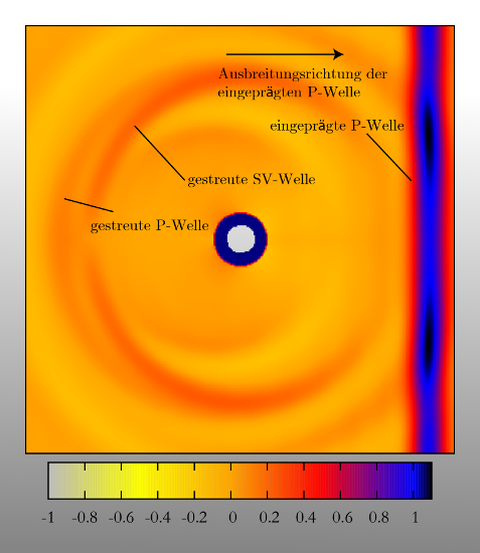
For the description of the dynamical behavior of composite materials such as, e.g., steel-, glass-, granitefiber reinforced concrete or carbon concrete the adequate modelling of the wave propagation through the material plays an important role. The stress waves propagating through the material are scattered at the boundaries between reinforcement or other inclusions and the surrounding matrix material. Thus, critical exposures may be exceeded locally which leads to an initiation of damage. The resulting microcracks may grow if the dynamic load holds on and finally the structural member or the whole structure may collapse. The description of the wave propagation takes into account the modelling of (partly) damaged bond behaviour and is performed both analytically and numerically.
References:
"ANALYTICAL DESCRIPTION OF FRC SUBJECTED TO TRANSIENT LOADS“, W. Weber, B. W. Zastrau, erschienen in "Journal of Theoretical and Applied Mechanics", Vol. 51, No. 1, S. 183-194; 2013
"NON-PLANE WAVE SCATTERING FROM A SINGLE ECCENTRIC CIRCULAR INCLUSION – PART I: SH WAVES", W. Weber, B. W. Zastrau, erschienen in "Journal of Theoretical and Applied Mechanics", Vol. 49, No. 4, S. 1183-1201; 2011
„Ein Beitrag zum Einfluss der Bewehrung auf die Körperwellenausbreitung in Verbundwerkstoffen“, erschienen in „Berichte des Instituts für Mechanik und Flächentragwerke“, Heft 5, TU Dresden, Fa-kultät Bauingenieurwesen, Dresden, 2011
Cooperation with:
Herr Prof. Dr. rer. nat. habil. Peter C. Müller (Bergische Universität Wuppertal)
Abstract:
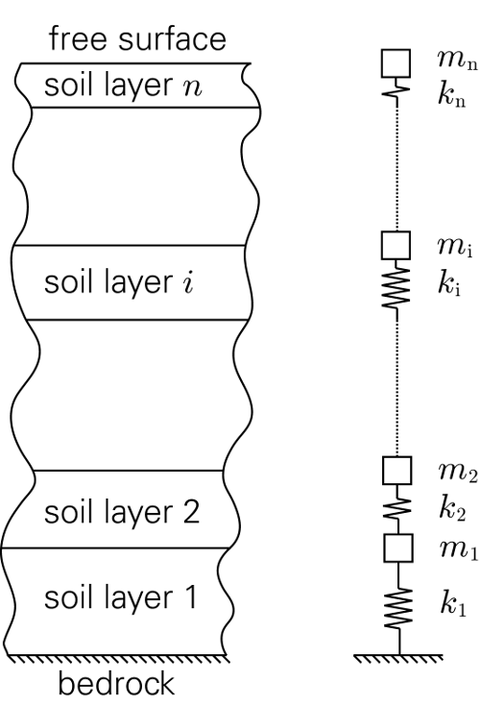
Dynamical systems with arbitrary degrees of freedom, e. g. vibration chains, play a tremendous role within mechanical investigations. For example, the dynamical behavior of layered soil subjected to earthquakes can efficiently be simulated using vibration chains. Herein, every layer of the soil is substituted by a mass and stiffness element. This way a vibration chain with a certain number of degrees of freedom is constituted and investigated within this research project. Special emphasis is on the eigenfrequencies and eigenmodes/ eigenforces, especially on their change if additional layers, i.e. masses, are added to the system.
References:
"CALCULATING THE RIGHT-EIGENVECTORS OF A SPECIAL VIBRATION CHAIN BY MEANS OF MODIFIED LAGUERRE POLYNOMIALS", W. Weber, B. Anders, B. W. Zastrau, erschienen in "Journal of Theoretical and Applied Mechanics, Sofia", Vol. 43, No. 4, S. 17-28, DOI: 10.2478/jtam-2013-0030; 2013
"A proof on eigenfrequencies of a special linear vibration system", W. Weber, B. Anders, P. C. Müller, erschienen in "Zeitschrift für Angewandte Mathematik und Mechanik", Vol. 95, No. 5, S. 519-526, DOI: 10.1002/zamm.201300058; 2015

Rollkontakt zwischen Rad und Schiene
Abstract:
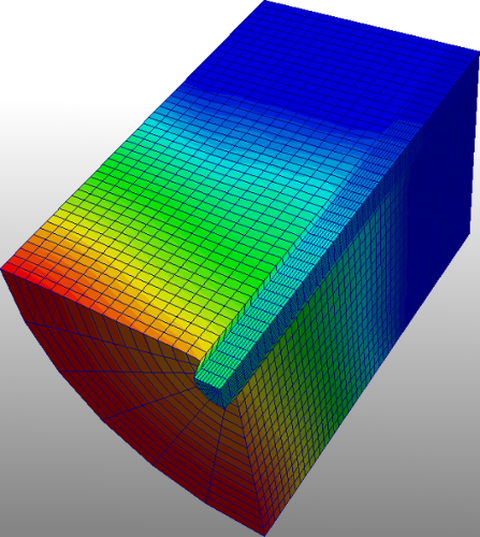
Scope of this project is the preparation of a suitable simulation tool for the numerical investigation of rolling contact phenomena. The main focus lies on the continuum–mechanical formulation of the mechanical field problem of contacting bodies and its numerical solution within the framework of the Finite Element Method. For reducing the numerical effort in rolling contact simulation, induced by the necessity of a very fine discretization within the expected contact area, a relative–kinematical description is utilized. This arbitrary LAGRANGian–EULERian approach is based upon the decomposition of the total motion into a rigid body motion and a superimposed deformation. The derivation of the equation of motion for the contact problem requires the relative-kinematical formulation of the continuum-mechanical fundamental equations, i. e. the balance equations and the constitutive relations. A suitable contact model including the contact of rough surfaces and varying contact boundary conditions is also necessary. The physical embedding into the environment is accomplished by NEUMANN and DIRICHLET boundary conditions.
Based upon that foundation the elastomechanics’ equations of motion are derived, which however can not be solved analytically in general. Hence, the equations of motion are transferred into their weak form by the application of the principle of virtual displacements serving for the numerical solution. The implementation of the problem demands for an incremental and discrete formulation of the equations, especially regarding the terms of inertia and the contact terms. Thereby, special attention has to be paid to the distinction between sticking and sliding within the framework of the tangential contact analysis. The numerical solution of the finite elements’ system of equations provides the state of stress, displacement and contact of two bodies in rolling contact. The reliability of the developed algorithms is finally verified by means of meaningful numerical examples for both static contact and for stationary rolling contact, whereby the numerical results coincide well with available analytical reference solutions.
References:
"Zur Finite-Element-Modellierung des stationären Rollkontakts von Rad und Schiene", Dissertation Dipl.-Ing. Sabine Damme, Heft 4 der Reihe "Berichte des IMF", 2006
@Inbook{Damme2003, author="Damme, Sabine and Nackenhorst, Udo and Wetzel, Anja and Zastrau, Bernd W.", editor="Popp, Karl and Schiehlen, Werner", chapter="On the Numerical Analysis of the Wheel-Rail System in Rolling Contact", title="System Dynamics and Long-Term Behaviour of Railway Vehicles, Track and Subgrade", year="2003", publisher="Springer Berlin Heidelberg", address="Berlin, Heidelberg", pages="155--174", isbn="978-3-540-45476-2", doi="10.1007/978-3-540-45476-2_10", url="http://dx.doi.org/10.1007/978-3-540-45476-2_10"}
V. Pauk, B. Zastrau, 2D rolling contact problem involving frictional heating, International Journal of Mechanical Sciences, Volume 44, Issue 12, December 2002, Pages 2573-2584, ISSN 0020-7403, http://dx.doi.org/10.1016/S0020-7403(02)00193-5.
“Advanced Contact Mechanics–Road and Rail”, Klaus Knothe , Ralf Wille , Bernd W. Zastrau, Vehicle System Dynamics, Vol. 35, Iss. 4-5, 2001, DOI: 10.1076/vesd.35.4.361.2043, 2001
Further information can be found in the detailed description.
link to research field "Damage and Fracture Mechanics"
link to research field "Mulitphysical Material Modelling on Multiple Scales"