Forschungsfeld "Numerische Methoden"
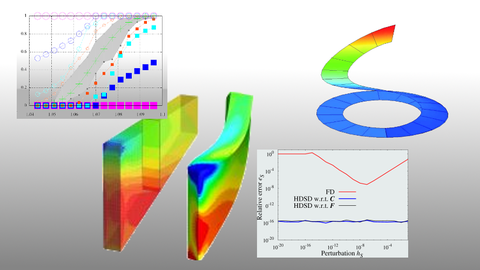
Viele Anwendungsfälle von Finite Elemente Methoden oder erweiterten Finite Elemente Methoden führen für „Standardelemente“ zu ungenauen Ergebnissen oder sind nicht robust. Am IMF werden daher numerische Methoden entwickelt, die zur Stabilisierung der XFEM bzw. zur Vermeidung von „Locking“-Effekten und zur Steigerung der Effizienz von Finite Elemente Technologien beitragen. Diese numerischen Methoden erhöhen so das Anwendungsspektrum von Finiten Elementen. Ein weiteres Forschungsfeld sind fehlerkontrollierte, adaptive Finite Elemente Methoden, mit denen sowohl eine Aussage über die Genauigkeit einer FEM / XFEM Simulation getroffen als auch die Diskretisierung und Modellierung der gewünschten Genauigkeit angepasst werden kann.
Forschungsprojekte
Ansprechpartner:
Stefan Löhnert
Abstrakt:
Bei der Berechnung von Rissen oder Heterogenitäten mit der XFEM kommt es vor, dass aufgrund der Lage der Diskontinuität bzw. aufgrund der gewählten Anreicherungsfunktionen nahezu lineare Abhängigkeiten zwischen einzelnen Freiheitsgraden entstehen können. Diese führen zu einer unter Umständen extrem schlechten Konditionierung des zu lösenden Gleichungssystems, was erhebliche numerische Probleme verursachen kann. In diesem Projekt werden daher Stabilisierungsmethoden entwickelt, um nahezu lineare Abhängigkeiten zu vermeiden bzw. die Konditionierung des Gleichungssystems zu verbessern ohne die Genauigkeit der Lösung zu beeinflussen. Die Methode basiert auf einer Singulärwertzerlegung der Elementsteifigkeitsmatrix von Elementen deren sämtliche Knoten angereichert sind. Alle Eigenmoden, deren Singulärwert eine Toleranz unterschreitet, werden stabilisiert. Physikalisch oder numerisch sinnvolle Null-Eigenmoden sind von der Stabilisierung ausgenommen. Da der Anteil an Elementen, deren sämtliche Knoten angereichert sind für die meisten Anwendungsfälle klein ist, bleibt der numerische Extraaufwand gering. Diese Regularisierung reduziert die Konditionszahl des resultierenden Gleichungssystems um mehrere Zehnerpotenzen.
Ansprechpartner:
Stefan Löhnert
Abstrakt:
Für nahezu inkompressible Materialien, wie z.B. Gummi oder viele Polymere sowie für Metalle im plastischen Bereich zeigen Finite Elemente mit Lagrange-Ansätzen niedriger Ordnung in der Regel locking-Effekte. Auch für XFEM Elemente kann unter diesen Umständen locking auftreten. Eine Möglichkeit, locking zu reduzieren oder ganz zu vermeiden ist, gemischte Ansätze zu verwenden. Diese Methoden haben sich für Finite Elemente bewährt. In diesem Projekt werden gemischte Methoden für die XFEM erweitert. Hierbei können unterschiedliche Anreicherungen, wie sie für Risssimulationen in der linear elastischen Bruchmechanik oder auch für die Simulation von Heterogenitäten bei kleinen und großen Deformationen genutzt werden, verwendet werden. Locking kann mit diesen gemischten XFEM Elementformulierungen vermieden werden, und die Konvergenzeigenschaften sind unabhängig von der Kompressibilität des Materials.
Ansprechpartner:
Stefan Löhnert, Jian Sun, Rohan Patel, Tengfei Lyu
Abstrakt:
Für nahezu inkompressible Materialien, wie z.B. Gummi oder viele Polymere sowie für Metalle im plastischen Bereich zeigen Finite Elemente mit Lagrange-Ansätzen niedriger Ordnung in der Regel locking-Effekte. Auch für XFEM Elemente kann unter diesen Umständen locking auftreten. Eine Möglichkeit, locking zu reduzieren oder ganz zu vermeiden ist, gemischte Ansätze zu verwenden. Diese Methoden haben sich für Finite Elemente bewährt. In diesem Projekt werden gemischte Methoden für die XFEM erweitert. Hierbei können unterschiedliche Anreicherungen, wie sie für Risssimulationen in der linear elastischen Bruchmechanik oder auch für die Simulation von Heterogenitäten bei kleinen und großen Deformationen genutzt werden, verwendet werden. Locking kann mit diesen gemischten XFEM Elementformulierungen vermieden werden, und die Konvergenzeigenschaften sind unabhängig von der Kompressibilität des Materials.
Abstrakt:
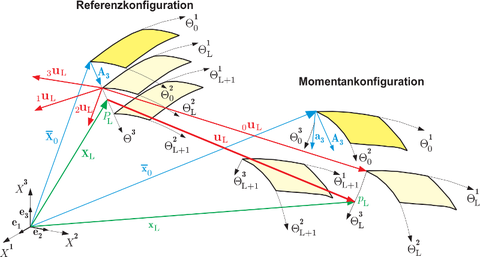
Im Rahmen dieser Forschungsarbeit wird die Formulierung eines mechanischen Modells in Verbindung mit der Umsetzung in ein Schalenelement im Rahmen der Finite-Element-Methode zur Simulation des Tragverhaltens geschichteter Flächentragwerksstrukturen unter Berücksichtigung der Schädigungsart Delamination vorgestellt. Grundlage des Mehrschichten-Modells ist die Entwicklung einer geometrisch nichtlinearen oberflächenorientierten Schalentheorie mit schub- und dickenelastischem Verhalten ausgehend von der vollständigen Kinematik einer Multidirektor-Theorie. Der Oberflächenbezug gewährleistet eine auf Kontaktprobleme angepasste mechanische Modellbildung. Innerhalb der Schichten wurde ein linear-elastisches orthotropes Materialgesetz verwendet, dessen Dreidimensionalität durch die Schalenformulierung nicht eingeschränkt wird. Das Hauptaugenmerk der Arbeit liegt auf der Entwicklung eines auf verschiedene Materialien anpassbaren Schichten-Verbundmodells. Das Versagen des Schichtenverbundes – Delamination genannt – wurde durch ein einfaches Spannungskriterium beschrieben. Der Delaminationsriss wird auf der Grundlage einer kontinuumsmechanischen Herangehensweise durch Modifikation der kinematischen Bedingungen berücksichtigt. Zur Beschreibung des Tragverhaltens nach Ausbildung des Delaminationsrisses wurde ein als „innerer Kontakt“ bezeichnetes Kontakt-Modell entwickelt, durch das Adhäsion zwischen den Schichten berücksichtigt werden kann. Das vorliegende Schalenmodell kann auf Probleme, in denen kleine Verschiebungen zu erwarten sind, für beliebige elastische Materialien angewendet werden. Der Rahmen, in dem diese Arbeit entstand, gab den hauptsächlichen Einsatzbereich, die Simulation von Flächentragwerksstrukturen mit einer Verstärkungsschicht aus textilbewehrtem Feinbeton, vor.
Referenzen:
Dissertation Jan Matheas, 2005, TU Dresden
DFG (Deutsche Forschungsgemeinschaft), Sonderforschungsbereich 528: Textile Bewehrungen zur bautechnischen Verstärkung und Instandsetzung
Teilprojekt C2: Verbundverhalten flächiger Verstärkungen
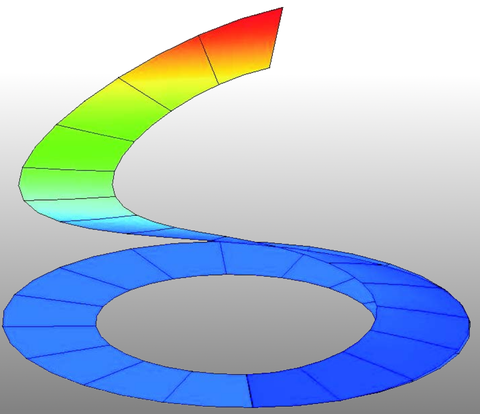
Verformte und verformte geschlitzte Kreisringplatte bei maximaler Last
Abstract:
Das Pojekt ist auf die theoretischen und numerischen Aspekte der Herleitung oberflächenorientierter Schalentheorien und Schalenelemente bzw. Volumen-Schalenelemente sowie ihrer Umsetzungen in ein leistungsstarkes Finite-Element-Programmpaket gerichtet. Kern der Arbeiten ist die Verwendung der Kontaktmechanik zur Beschreibung des Schichtenverbundes insbesondere im Zusammenhang mit oberflächenorientierten Mehrschichten-Multidirektor-Schalenelementen. Im Vordergrund steht die Ermittlung von Kontaktspannungszustand und Delamination, zum einen zwischen Grundmaterial und Verstärkung, zum anderen in beliebigen Flächen der Schichtengrenzen innerhalb der Verstärkung.
Weitere Informationen sind der Detailbeschreibung zu entnehmen.
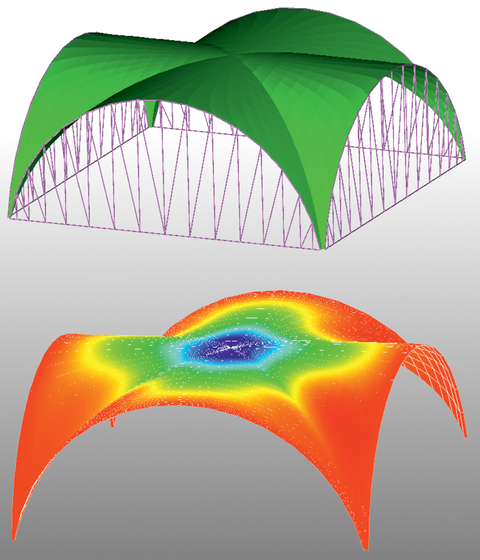
Verformungsberechnung eines Schalentragwerkes in Form eines Kreuzgewölbes mit quadratischer Grundfläche
Abstract:
DREFES ist eine Adaption des Programms FEABL, das ursprünglich am Department of Aeronautics and Astronautics des Massachusetts Institute of Technology (USA) entwickelt wurde. Es handelt sich um eine Software, die Finite-Elemente-Berechnungen ermöglicht. Die Simulationssoftware ist im Laufe der Zeit u.a. um diverse Schalen-Elemente, insbesondere um oberflächenorientierte Mehrschichten-Multidirektor-Schalenelemente erweitert worden. Sie kann zur numerischen Simulation von textilbetonverstärkten flächigen Bauteilen verwendet werden, wobei Delamination und Kontakt in der Simulation erfasst werden können.
Weitere Informationen sind der Detailbeschreibung zu entnehmen.
zum Forschungsfeld "Schädigungs- und Bruchmechanik"
zum Forschungsfeld "Multiphysikalische Materialmodellierung auf mehreren Skalen"
zum Forschungsfeld "Dynamik der Kontinua"
zum Forschungsfeld "Fachdidaktik der Ingenieurwissenschaften"