New Methods for Reliability-Based Design Optimization of Multiphase Steel Components
Abstract of the planned project content, taking into account the results from the first project phase
Modeling the influence of multiple uncertainties is a fundamental problem for the optimization of tailored, crash-relevant car parts, and also for their numerical structural analysis itself. These uncertainties are associated with the material properties, which are dominated by uncertainties on a lower scale, with the production process, and with the loading scenarios to be expected during the lifetime of the component. Especially as a result of the tailoring strategies such as the concept of tailored blanks or local laser hardening, important material properties for the crash safety vary over time due to cyclic loading under normal operation conditions, which leads to rather large additional uncertainties for the analysis of the crash scenario. Therefore, in this project the main goal is to develop methods for the reliability-based design optimization of tailored, crash-relevant car components under polymorphic uncertainties. The major target therein is to maximize performance measures while prescribing maximally acceptable values of upper bounds on the probability of failure (PoF). The methods will be based on a Dirac mass discretization of the epistemic uncertainties and thereby, no assumptions regarding the type of distribution functions for these uncertainties need to be made.
The aleatoric uncertainties are included through a nested approach taking advantage of improved Monte-Carlo methods and specialized surrogate models. The Dirac mass discretization will be extended with respect to the following aspects: (i) Combination with fuzzy variables to describe epistemic design parameters, (ii) incorporation into the concept of alpha-level discretizations, and (iii) enhancement to account for optimal bounds on propagated uncertainties related with the performance measures to be optimized.
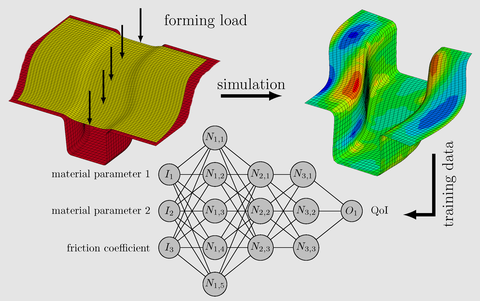
For the computation of the performance measures and the quantity of interest defining failure, a realistic computational model will be constructed which includes the relevant parts of the production process, for instance to account for the eigenstresses induced by the metal forming procedure. In addition to that, a new method will be developed to incorporate the local variation of material properties by surrogate models using neural networks based on random field realizations. These will be obtained by the data-based identification of real property maps and the construction of realizations which match the real property distributions and correlations. By including a double-nested Monte-Carlo analysis, the uncertainties of the model itself used for the training of the neural network will be controlled. The developed methods will be analyzed in the context of realistic optimization problems of car parts under crash loads as well as benchmark problems defined in SPP 1886.
Essential project goals and objectives
- Combination of multiobjective optimization and OUQ
- Combination of OUQ and fuzzy sets and implementation of uncertainty propagation
- Construction of surrogate models for random fields
- Computation of benchmark problems
Prof. Dr.-Ing. habil. Daniel Balzani
Ruhr-Universität Bochum
Lehrstuhl für Kontinuumsmechanik