Forschungsfelder
Inhaltsverzeichnis
Reglerentwurf für lineare und nichtlineare Systeme
Dynamische Systeme sind in der Natur und Technik omnipräsent: Ein Gebäude kühlt nach dem Abschalten der Heizung langsam auf Umgebungstemperatur ab, der Füllstand eines Tanks mit konstantem Zulauf steigt linear mit der Zeit, ein Elektromotor erreicht nach dem Einschalten der Spannung asymptotisch eine bestimmte Drehzahl. Stets verändern sich relevante Systemvariablen mit der Zeit in Abhängigkeit von Eingangssignalen. Um ein gewünschtes Verhalten zu erreichen (z.B. Solltemperatur, -füllstand, -drehzahl), ist es notwendig, diese Eingangssignale in Abhängigkeit der aktuellen Systemgrößen geeignet zu wählen. Mit anderen Worten: Für ein gegebenes (lineares oder nichtlineares dynamisches System) muss ein passender Regelalgorithmus entworfen werden.
Beispiele:
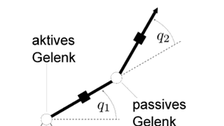
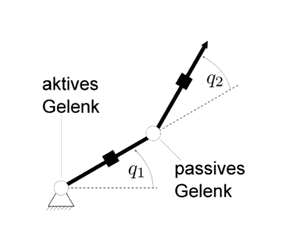
Ein mechanisches System nennt man unteraktuiert, wenn die Anzahl der Stelleingriffe (eingeprägte Kräfte bzw. Momente) kleiner ist als die Anzahl der mechanischen Freiheitsgrade. Stimmt dagegen die Anzahl der Stelleingriffe mit der Anzahl der mechanischen Freiheitsgrade überein, so spricht man von vollständig aktuierten bzw. vollständig direkt gesteuerten Systemen. Während die Modellierung bei beiden Systemklassen (unteraktuiert bzw. vollständig aktuiert) in der gleichen Weise mit den gängigen Methoden der Starrkörpermechanik erfolgen kann (z.B. Newton, Euler-Langrange, Hamilton), sind unteraktuierte Systeme regelungstechnisch meist deutlich schwerer zu beherrschen als vollständig aktuierte Systeme. Der Übergang zu einem unteraktuierten System würde aus technischer Sicht der gezielten Einsparung von Antrieben entsprechen und damit eine Möglichkeit zur Material- bzw. Kosteneinsparung eröffnen. Für Spezialanwendungen (z.B. in der Weltraumtechnik) könnte auch die Gewichtsreduktion relevant sein. Ebenso kann es notwendig sein, bestimmte Systeme auch im Fall eines Aktordefekts noch gezielt beeinflussen zu können.
Beispiel: Unteraktuierter ebener Zweigelenkmanipulator:

© C. Knoll (TU Dresden)
© C. Knoll
Veröffentlichungen:
- Knoll, C. & Röbenack, K.: Control of an underactuated manipulator using similarities to the double integrator. Preprints of the 18th IFAC World Congress, 2011, 11501-11507.
- Knoll, C.; Leist, B. & Röbenack, K.: Konzeption und prototypische Realisierung eines Versuchsstandes zur Regelung eines unteraktuierten Manipulators. In: Bertram, T.; Corves, B. & Janschek, K. (Hrsg.), Tagungsband Mechatronik 2011, 2011, 241-246.
- Knoll, C. & Röbenack, K.: Trajectory Planning for a Non Flat Mechanical System Using Time-Reversal Symmetry. Proc. in Applied Mathematics and Mechanics, 2011, 11, 819?820
- Knoll, C. & Röbenack, K.: Sliding Mode Control of an Underactuated Two-Link Manipulator. Proc. in Applied Mathematics and Mechanics, 2010, 10, 615-616.
- Knoll, C. & Röbenack, K.: Analysis and Control of an Underactuated Pendulum. Proc. 55. Internationales Wissenschaftliches Kolloquium, Ilmenau, 2010, 440-451
Typischerweise werden Regler zur Stabilisierung von Ruhelagen entworfen. Bedingt durch nicht modellierte diskontinuierliche Effekte (z. B. Hysterese, Lose, Totzone, ...) stellen sich beim praktischen Einsatz trotzdem Schwingungen ein. Als Alternative zum Reglerentwurf für eine Ruhelage stellen wir einen Ansatz vor, bei dem ein nichtlinearer Zusandsregler einen gewünschten Grenzzyklus in das System einbringt und stabilisert. Bei diesem Grenzzyklus sind Frequenz, Amplitude und Einschwingverhalten gezielt vorgebbar. Die entwickelte Entwurfssystematik wurde an verschiedenen Systemen simulativ verifiziert und am Versuchsstand eines beweglich gelagerten inversen Pendels experimentell erprobt.
Veröffentlichungen:
- Knoll, C.; Röbenack, K.: Generation of stable limit cycles with prescribed frequency and amplitude via polynomial feedback.
- In: Proc. of the 9th International Multi-Conference on Systems, Signals and Devices, Chemnitz, 2012. Best Paper Award.
- Knoll, C.; Röbenack, K. (2012), Orbital stabilization of a class of underactuated mechanical systems. Proc. Appl. Math. Mech. (PAMM), 12: 711-712. doi: 10.1002/pamm.201210344.
- Knoll, C.; Röbenack, K.: Robust Generation of Desired Periodic Orbits: From Electrical Oscillators in the Phase Plane to Underactuated Systems of Higher Order. In: Proc. Nonlinear Dynamics of Electronic Systems 2012 (NDES 2012), S. 78-81, Wolfenbüttel, 2012.
- Röbenack, K.; Knoll, C.: Erzeugung von stabilen Grenzzyklen mittels Rückführung bei vorgegebener Frequenz und Amplitude. Vortrag beim GAMM-Fachausschuss "Dynamik und Regelungstheorie", Magdeburg, 26.-27.09.2013.
- Knoll, C.; Röbenack, K.: Stable Limit Cycles with Specified Oscillation Parameters Induced by Feedback: Theoretical and Experimental results. Transactions on Systems, Signals and Devices, 2013, vol. 8, no. 1, pp. 127-144, Shaker Verlag, Aachen. ISBN: 978-3-8440-2254-4.
- Knoll, C.; Röbenack, K.: Gezielte Erzeung und Stabilisierung von Grenzzyklen durch nichtlineare Rückführungen. Vortrag bei den Dresdner Automatisierungstechnische Kolloquien, 273. Kolloquium, 27.01.2014.
Kennt man für ein nichtlineares System einen flachen Ausgang, dann vereinfacht diese Kenntnis den Entwurf von Vorsteuerungen bzw. Regelung erheblich. Die Überprüfung eines konkreten Systems auf Flachheit bzw. das Auffinden eines flachen Ausgangs gestaltet sich dagegen in der Regel wesentlich komplizierter. In [1] werden einige Spezialfälle behandelt. Ein sehr allgemeines Verfahren zum Auffinden flacher Ausgänge wird in [2] beschrieben und an mehreren Beispielen illustriert.
Veröffentlichungen:
- Franke, M. & Röbenack, K.: Some remarks concerning differential flatness and tangent systems. Proc. in Applied Mathematics and Mechanics, 2012, 12(1), S. 729-730.
- Franke, M. & Röbenack, K.. On the Computation of Flat Outputs for Nonlinear Control Systems. Proc. European Control Conference (ECC) 2013, S. 167-172.
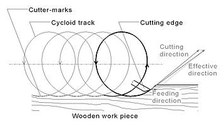
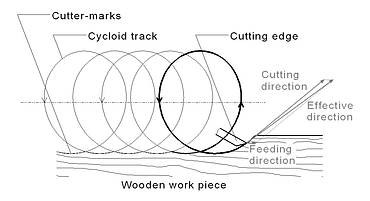
Spanungsprozesse, bei denen die Richtungen der Vektoren der Schnitt- und Vorschubbewegung nicht gleich sind, erzeugen auf den gefertigten Flächen am Werkstück sehr oft spezielle prozessbedingte, regelmäßige kinematische Oberflächentopografien. Dies trifft z. B. auf Umfangsfräsverfahren zu, wobei hier sogenannte Messer- oder Hobelschläge entstehen. Man spricht in diesem Zusammenhang von einer kinematischen Rauheit bzw. Welligkeit. Die Gestalt der Oberfläche, die durch diese periodische Bearbeitungsspuren gekennzeichnet ist, muss in vielen Fällen als gegeben hingenommen werden und kann nur durch präzise Schneideneinstellung und angepasste Wahl der kinematischen Einstellgrößen (Werkzeugdrehzahl, Vorschubgeschwindigkeit, Schneidenzahl) minimiert werden. Eine Reihe von Feinbearbeitungsverfahren (Finieren, Schleifen) werden anschließend eingesetzt, um diese topografischen Abweichungen von der gewünschten ebenen Gestalt der gefertigten Fläche zu egalisieren.
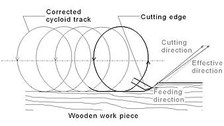
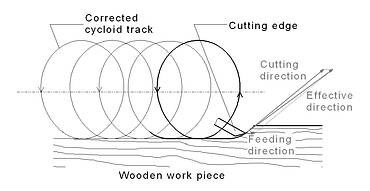
Die Topografie der Messerschläge auf dem Werkstück resultiert aus den Werkzeug- und Werkstückbewegungsverhältnissen, die durch regelmäßige, periodische Bewegungsbahnen einer verlängerten Zykloide entsprechen (Abbildung links). Basierend auf einer Idee des Institutes für Holz- und Papiertechnik der TU Dresden, soll ein neuartiger Stellmechanismus an der Werkzeugschnittstelle (Lagerung) entwickelt werden, welcher die in der Ausgangssituation beschriebenen gegenwärtigen Zustände beim Umfangsfräsen verbessern kann. Dabei wird über eine komplette Werkzeugverschiebung im Mikrobereich eine generelle Flugkreiskorrektur bzw. eine phasenweise gesteuerte Flugbahnanpassung realisiert. Diese Verstellung soll letztendlich zu einer Minimierung der Messerschläge und zu einer Verringerung des schlagartigen Eingreifens der Schneide ins Werkstück führen. Es ist angedacht, im Eingriffsbereich der späteren gefertigten Werkstückoberfläche die Flugbahn der Schneide am Werkzeug kurzzeitig einer linearen Schnittbewegung anzupassen. Die geringen radialen Stellwege von wenigen Mikrometern sollen durch geeignete, heute verfügbare elektromechanische oder andere Aktoren (bspw. Piezoaktoren) an der Werkzeugschnittstelle bzw. -lagerung realisiert werden. Eine Möglichkeit zur Kompensation der bogenförmigen Wirkbewegung beim Umfangsfräsen besteht in der entsprechenden linearen Bewegung des kompletten Umfangsfräswerkzeuges in der Arbeitsebene senkrecht zur Vorschubrichtung (Abbildung rechts).
© Gottlöber, TU Dresden
© Gottlöber, TU Dresden
Veröffentlichungen:
- Gottlöber, C.; Röbenack, K.; Ahmed, D. & Eckhardt, S.: An Approach for Actuator Controlled Motion of Peripheral Milling Tools on Wood. International Journal of Engeineering Research and Applications (IJERA), 2012, 2, 1208-1213
- Röbenack, K.; Ahmed, D.; Eckhardt, S. & Gottlöber, C.: Peripheral Milling of Wooden Materials without Cutter-Marks - A Mechatronic Approach. WSEAS Transactions on Applied and Theoretical Mechanics, 2013, 8(2), 170-179.
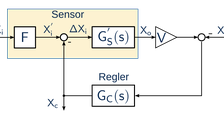
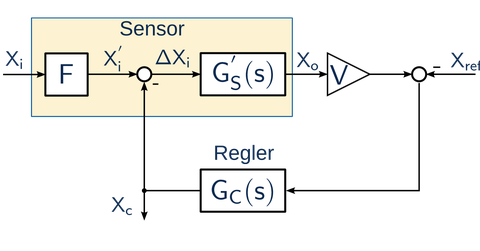
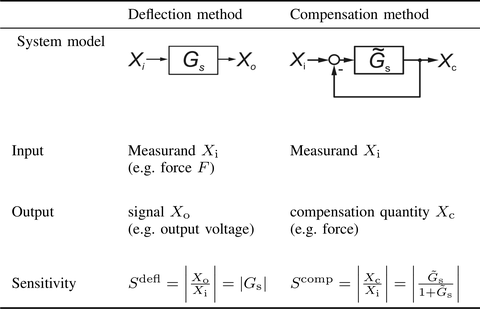
In Zusammenarbeit mit dem Institut für Festkörperelektronik der TU Dresden wurden für den Entwurf von Sensoren die Ausschlagsmethode (deflection method) und die Kompensationsmethode miteinander verglichen. Bei der Kompensationsmethode ist ein Regler zu entwerfen. Für P-, PI- und PID-Regler wurden systematische Entwurfskriterien angegeben und katalogisiert. Grundsätzlich sit die vorgeschlagene Methode auch bei bestimmten Klassen nichtlinearier Systemmodelle anwendbar (z.B. auf Basis des Satzes der kleinen Kreisverstärkung oder des Stabilitätstests von Popov).
© K. Röbenack
© K. Röbenack
Veröffentlichung:
- Schulz, V.; Gerlach, G.; Röbenack, K.: Compensation method in sensor technology: a system-based description. Journal of Sensors and Sensor Systems, 2012, 1, 5-27.
Beobachterentwurf für nichtlineare Systeme
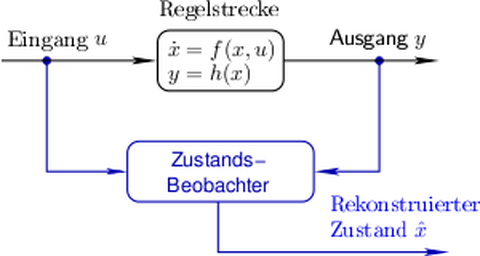
Dieser Forschungsschwerpunkt widmet sich dem Entwurf von Beobachtern zur Ermittlung schlecht oder nicht messbarer Prozessgrößen. Derartige Einrichtungen zur modellbasierten Rekonstruktion von Prozessgrößen werden mitunter auch als Software-Sensoren bezeichnet. Die zugrunde liegenden Modelle sind nichtlinear. Es werden sowohl klassische Zustandsbeobachter als auch Beobachter zur Rekonstruktion der Eingangssignale untersucht. Die entwickelten Entwurfsverfahren kombinieren differential-geometrische Zugänge mit High-Gain-Ansätzen.
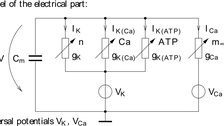
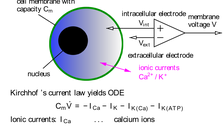
Ein vielversprechendes Anwendungsgebiet dieser Techniken ist die Zellbiologie. Die dort auftretenden Modelle zeichnen sich durch außerordentlich komplizierte Nichtlinearitäten aus. Die direkte Messung verschiedener Größen (z.B. Ionenströme durch eine Zellmembran) beeinflussen die Wechselwirkung der Zelle mit anderen Zellen. Zur Schätzung solcher Größen wurden Beobachter/Filter-Kombinationen vorgeschlagen bzw. Residuengeneratoren eingesetzt.
Beispiele:
Beobachter dienen der Ermittlung schlecht oder nicht messbarer Prozessgrößen. Derartige Einrichtungen zur modellbasierten Rekonstruktion von Prozessgrößen werden mitunter auch als Software-Sensoren bezeichnet. Die zugrunde liegenden Modelle sind nichtlinear. Es werden sowohl klassische Zustandsbeobachter als auch Beobachter zur Rekonstruktion der Eingangssignale untersucht. Die entwickelten Entwurfsverfahren kombinieren differential-geometrische Zugänge mit High-Gain-Ansätzen.
Der Beobachterentwurf gestaltet sich besonders einfach, wenn das System in die Beobachter-Normalform transformiert werden kann. In dieser Normalform treten die Nichtlinearitäten nur als Ausgangsaufschaltung in Abhängigkeit vom gemessenen Ausgang (und ggf. dem gemessenen Eingang) auf. Diese Entwurfsmethodik wurde 1983 von Bestle und Zeitz (Bestle, D.; Zeitz, M.: Canonical form observer design for non-linear time-variable systems. Int. J. Control, 1983, 38, 419-431) sowie von Krenen und Isidori (Krener, A. J.; Isidori, A.: Linearization by output injection and nonlinear observers. Systems & Control Letters, 1983, 3, 47-52) vorgestellt. Die Schwierigkeit besteht in den restriktiven Existenzbedingungen der Beobachter-Normalform bzw. ihrer komplizierten Berechnung. Als Ausweg bietet sich der erweiterte Luenberger-Beobachter an, bei dem die Fehlerdynamik in der Normalform linearisiert wird (Zeitz, M.: The extended Luenberger observer for nonlinear systems. Systems & Control Letters, 1987, 9, 149-156). Dieser Ansatz wurde auf eine beliebige Approximationsordnung erweitert. Außerdem konnten globale Konvergenzbedingungen für den erweiterten Luenberger-Beobachter angegeben werden.
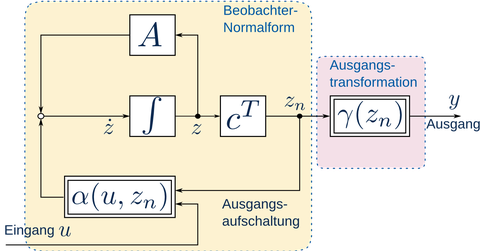
Nichtlineare Beobachter-Normalform mit Ausgangstransformation
Veröffentlichungen:
- Röbenack, K.; Lynch, A. F.: An efficient method for observer design with approximately linear error dynamics. International Journal of Control, 2004, 77, 607-612
- Röbenack, K.: Entwurfsmethodik für einen approximativen Normalform-Beobachter. Proc. in Applied Mathematics and Mechanics, 2004, 4, 137-138
- Röbenack, K.: Approximate Observer Error Linearization for Multi-Output Systems. Preprints of the 16th IFAC World Congress, Prague, Czech Republic, July 3-8, 2005
- Röbenack, K.: Direct Approximation of Observer Error Linearization for Nonlinear Forced Systems. IMA Journal of Mathematical Control and Information, 2007, 24, 551-566
- Röbenack, K.: Entwurf nichtlinear Beobachter mit linearer und näherungsweise linearer Fehlerdynamik. Automatisierungstechnik, 2010, 58, 489-497
- Röbenack, K.: A Flow-Based Approximation of Observer Error Linearization for Non-Linear Systems. WSEAS Transactions on Systems and Control, 2013, 8(1), 11-20.
Die Existenzbedingungen für eine exakte Linearisierung des Beobachtungsfehlers sind sehr restriktiv und daher in vielen praktischen Anwendungsfällen nicht erfüllt. Als Alternative bietet sich in diesen Fällen eine partielle Linearisierung da, d.h. eine Linearisierung bezogen auf eine geeignete Untermannigfaltigkeit des Zustandsraums.
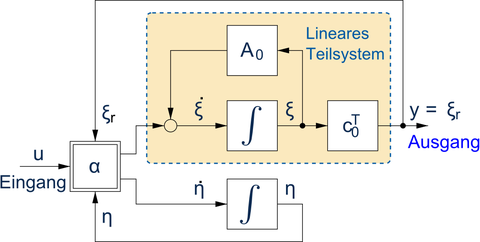
Partielle Beobachter-Normalform
Veröffentlichungen:
- Röbenack, K.: Zum High-Gain-Beobachterentwurf für eingangs-ausgangs-linearisierbare SISO-Systeme. Automatisierungstechnik, 2004, 52, 481-488
- Röbenack, K.; Lynch, A. F.: Observer Design Using a Partial Nonlinear Observer Canonical Form. Applied Mathematics and Computer Science, 2006, 16, 333-343
- Röbenack, K.: Extended Luenberger Observer for Nonuniformly Observable Nonlinear Systems. In: Meurer, T.; Graichen, K.; Gilles, E. D. (Hrsg.), Control and Observer Design for Nonlinear Finite and Infinite Dimensional Systems, Springer, 2006, 322, 19-34
- Röbenack, K.: Observer Design for a Class of Nonlinear Systems with Non-Full Relative Degree. Nonlinear Dynamics and Systems Theory, 2007, 7, 399-408
Die Idee der High-Gain-Beobachter besteht darin, mit einer ausreichend starken linearen Fehleraufschaltung die Nichtlinearitäten des zu beobachtenden Systems zu dominieren. Dieser Ansatz wurde F. E. Thau zurück (Thau, F. E.: Observing the state of nonlinear dynamical systems. Int. J. Control, 1973, 17, 471-479).
Veröffentlichungen:
- Röbenack, K.: Zum High-Gain-Beobachterentwurf für eingangs-ausgangs-linearisierbare SISO-Systeme. Automatisierungstechnik, 2004, 52, 481-488.
- Röbenack, K.: Computation of High Gain Observers for Nonlinear Systems using Automatic Differentiation. Journal Dynamic Systems, Measurement, and Control, 2005, 127, 160-162.
- Röbenack, K.: High Gain Observers Using an Approximate Observer Normal Form. Proc. in Applied Mathematics and Mechanics, 2006, 6, 837-838.
- Röbenack, K.; Lynch, A. F.: High-Gain nonlinear observer design using the observer canonical form. IET Control Theory & Applications, 2007, 1, 1574-1579.
- Röbenack, K.: Structure Matters -- Some Notes on High Gain Observer Design for Nonlinear Systems. Proc. of the 9th International Multi-Conference on Systems, Signals and Devices (SSD 2012), Chemnitz, 20-23 March 2012.
Der Czochralski-Kristallzüchtungsprozess ist eines der wichtigsten Verfahren zur Herstellung einkristalliner Formkörper, aus denen Wafer für die Weiterverarbeitung in der mikro- und optoelektronischen Industrie geschnitten werden. Der Verlauf des Kristalldurchmessers muss dabei geeigntene Trajektorien folgen, damit wichtige technologische Rahmenbedingungen erfüllt werden. Eine entsprechende Regelung ist daher unerlässlich.
Unglücklicherweise ist der Kristalldurchmesser nicht direkt meßbar. Häufig steht lediglich die Kraft, die der Kristall und die Schmelzzone auf eine an der Ziehstange angebrachte Wägezelle ausübt, als Meßsignal zur Verfügung. Aus diesem sind auf Basis eines entsprechenden Modells der Kristalldurchmesser und andere wichtige Kenngrößen des Prozesses zu rekonstruieren. Am Institut werden hierzu verschiedene Verfahren entwickelt, untersucht und im praktischen Experiment erprobt. Dabei gilt es auch, Fragestellung zur Robustheit gegenüber Parameterunbestimmtheiten und Meßsignalstörungen zu beachten.

Germanium-Kristall, gezogen mit Hilfe eines Zustandsbeobachters und automatischer Durchmesserregelung
Veröffentlichungen:
- Winkler, J., Röbenack, K.: Observer based determination of the crystal diameter in Czochralski crystal growth utilizing algorithmic differentiation. Proc. of the 9th International Multi-Conference on Systems, Signals and Devices (SSD 2012), Chemnitz, 20-23 March 2012.
- Winkler, J., Neubert, M., Rudolph, J.: Nonlinear model-based control of the Czochralski process I: Motivation, modeling and feeback controller design. Journal of Crystal Growth 312 (2010) 1005-1018
- Winkler, J., Neubert, M., Rudolph, J.: Nonlinear model-based control of the Czochralski process II: Reconstruction of crystal radius and growth rate from the weighing signal. Journal of Crystal Growth 312 (2010) 1019-1028
- Winkler, J.;Lindert, S.-O.; Röbenack, K.; Rudolph, J.: Design of a nonlinear observer using automatic differentiation. Proc. in Applied Mathematics and Mechanics 4, 2004, S. 147-148
Aufgrund des ständig steigenden Transportaufkommens sind lange Lastzügen gefordert. Zur Erhaltung der Manövrierfährigkeit werden bei diesen Transpostsystemen mehrere Achsen aktiv gelenkt. Für Steer-by-Wire-Lenkungen und Manöverassistenz ist die Kenntnis der eigenen Fahrzeugspur unerlässlich. Dazu werden Filter- und Beobachteransätze unter Berücksichtigung verschiedener Sensorkonstellationen untersucht.
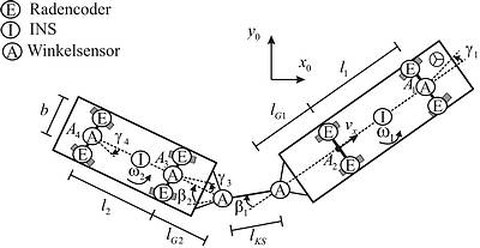
Modell und Sensorkonfiguration des Versuchsfahrzeuges
Veröffentlichungen:
- Huber, R.; Jäkel, J.; Zipser, S.; Wagner, S.: Track estimation for multi-axle steered truck-trailer vehicles. Proc. of the 12th Mechatronics Forum Biennial International Conference, Zurich, September 2010, S. 294-301.
- Huber, R.; Röbenack, K.; Zipser, S.; Wagner, S. : Beobachterentwurf zur Spurschätzung eines mehrachsgelenkten Fahrzeuges. In: Bertram, T.; Corves, B.; Janschek, K. (Hrsg.) Tagungsband Mechatronik 2011, 2011, 43-48.
- Huber, R.; Zipser, S.; Wagner, S.; Röbenack, K.: Fault-Tolerant track estimation algorithm for truck-trailer vehicles. Proc. 56th International Scientific Colloquium, 2011.
- Huber, R.; Zipser, S.; Wagner, S.; Röbenack, K.: A high-gain observer vs. algebraic derivative methods for track estimation. Proc. of the 9th International Multi-Conference on Systems, Signals and Devices (SSD 2012), Chemnitz 20-23 march 2012.
Ein vielversprechendes Anwendungsgebiet dieser Techniken ist die Zellbiologie. Die dort auftretenden Modelle zeichnen sich durch außerordentlich komplizierte Nichtlinearitäten aus. Die direkte Messung verschiedener Größen (z.B. Ionenströme durch eine Zellmembran) beeinflussen die Wechselwirkung der Zelle mit anderen Zellen. Zur Schätzung solcher Größen wurden Beobachter/Filter-Kombinationen vorgeschlagen bzw. Residuengeneratoren eingesetzt.
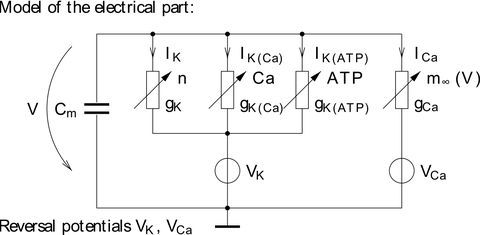
© K. Röbenack
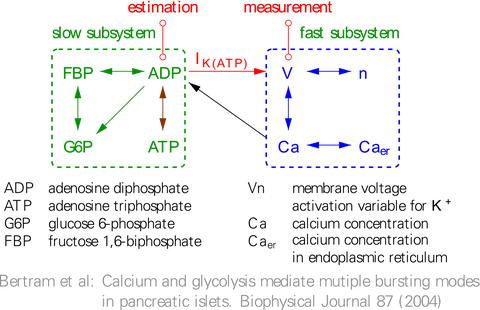
© K. Röbenack
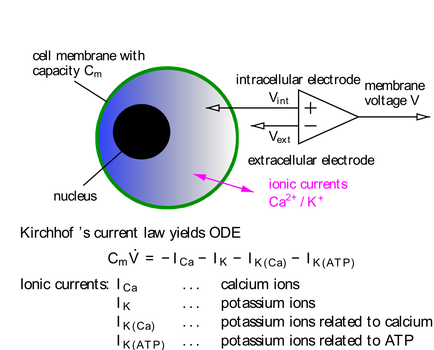
© K. Röbenack
Veröffentlichungen:
- Röbenack, K.; Goel, P.: Observer Based Measurement of the Input Current into A Neuron. Mediterranean Journal of Measurement and Control, 2007, 3, 22-29
- Röbenack, K.; Goel, P.: A combined observer and filter based approach for the determination of unknown parameters. International Journal of Systems Science, 2009, 40, 213-221
- Röbenack, K.: Residual Generator based Measurement of the Current Input into a Cell. Nonlinear Dynamics and Systems Theory, 2009, 9, 425-434
- Röbenack, K.: Observer based measurement of the Adenosine Diphosphate concentration in multimodal oscillatory pancreatic β-cells. Proc. 18th IEEE Workshop on Nonlinear Dynamics of Electronic Systems (NDES2010), 2010, 54-57
Simulation und Realisierung von Regelungseinrichtungen mit algorithmischem Differenzieren
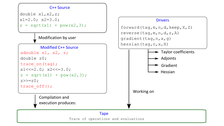
Zahlreiche Entwurfsverfahren zur Regelung nichtlinearer Systeme basieren auf differentialgeometrischen Ansätzen. Für die konkrete Auslegung und Implementierung der jeweiligen Regelungseinrichtung werden oft Lie-Ableitungen benötigt. In vielen Fällen kann man die gewünschten Ableitung mit Computer-Algebra-Software symbolisch berechnen. Benötigt man höhere Ableitungen, dann wächst die Größe der entstehenden Ausdrücke in der Regel exponentiell an. Alternativ kann man Ableitungen numerisch mit Differenzenquotienten berechnen. Die Genauigkeit der Ableitung hängt maßgeblch von der gewählten Schrittweite ab. Selbst bei einer optimalen Schrittweite verliert die so gewählte Ableitung gegenüber dem Funktionswert an Genauigkeit.
Beim algorithmischen oder automatischen Differenzieren (AD) muss die zu differenzierende Funktion als Algorithmus in einer geeigneten Programmiersprache vorliegen. Die Ableitung wird ähnlich wie beim symbolischen Differenzieren durch systematisches Anwenden der Ableitungsregeln bestimmt. Allerdings werden die Zwischenergebnisse nicht als symbolischer Teilausdruck weitergereicht, sondern als Gleitkommazahl. Im Programmpaket ADOL-C wird das algorithmische Differenzieren mit Hilfe von Operatorüberladung implementiert.
Buchveröffentlichungen:
- Röbenack, K.: Beobachterentwurf für nichtlineare Zustandssysteme mit Hilfe des Automatischen Differenzierens. Shaker Verlag, 2003 (ISBN: 978-3-8322-1069-4)
- Röbenack, K.: Regler- und Beobachterentwurf für nichtlineare Systeme mit Hilfe des Automatischen Differenzierens. Shaker Verlag, 2005 (ISBN: 978-3-8322-4414-9)
Beispiele:
Allgemein sind Lie-Ableitungen für Tensorfelder definiert und können als Ableitungen entlang der Lösung dynamischer Systeme interpretiert werden. In der nichtlinearen Regelungstechnik benötigt man je nach Anwendung Lie-Ableitungen von Skalar-, Vektor- und Kovektorfeldern.
Veröffentlichungen:
- Röbenack, K.: On the efficient computation of higher order maps adkf g(x) using Taylor arithmetic and the Campbell-Baker-Hausdorff formula. In: Zinober, A.; Owens, D. (Hrsg.), Nonlinear and Adaptive Control, Springer, 2002, 281, 327-336
- Röbenack, K.; Reinschke, K. J.: The Computation of Lie Derivatives and Lie Brackets based on Automatic Differentiation. Zeitschrift für Angewandte Mathemaik und Mechnik (ZAMM), 2004, 84, 114-123
- Röbenack, K.: Computation of Lie Derivatives of Tensor Fields Required for Nonlinear Controller and Observer Design Employing Automatic Differentiation. Proc. in Applied Mathematics and Mechanics, 2005, 5, 181-184
- Röbenack, K.: Computational of multiple Lie derivatives by algorithmic differentiation. Journal of Computational and Applied Mathematics, 2008, 213, 454-464
- Röbenack, K.: Computation of mixed Lie derivatives in nonlinear control. Proc. in Applied Mathematics and Mechanics, 2010, 10, 627-628
- Röbenack, K.; Winkler, J.; Wang, S.: LIEDRIVERS - A Toolbox for the Efficient Computation of Lie Derivatives Based on the Object-Oriented Algorithmic Differentiation Package ADOL-C. In: Proc. of the 4the International Workshop on Equations-Based Object-Oriented Modeling Languages and Tools (EOOLT 2011), 57-66. Zurich, Switzerland, September 5, 2011. ISSN: 1650-3686.
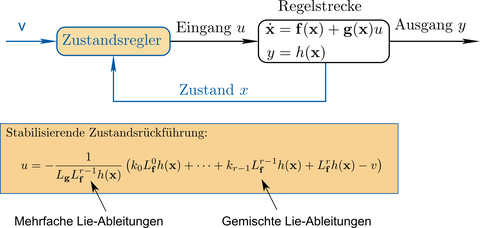
Beim Reglerentwurf mittels exakter Eingangs-Ausgangs-Linearisierung benötigt man mehrfache und eine gemischte Lie-Ableitung eines Skalarfeldes. Die zugehörigen Funktionswerte dieser Lie-Ableitungen lassen sich sehr leicht mit Hilfe des algorithmischen Differenzierens bestimmen.
Veröffentlichungen:
- Röbenack, K.; Reinschke, K. J.: Reglerentwurf mit Hilfe des Automatischen Differenzierens. Automatisierungstechnik. 2000, 48, 60-66
- Röbenack, K.; Vogel, O.: Computation of state and input trajectories for flat systems using automatic differentiation. Automatica, 2004, 40, 459-464
- Röbenack, K.: Automatic Differentiation and Nonlinear Controller Design by Exact Linearization. Future Generation Computer Systems, 2005, 21, 1372-1379
- Röbenack, K.: Nonlinear controller design based on algorithmic plant description. Mathematical and Computer Modelling of Dynamical Systems, 2007, 13, 193-209
Die Beobachtbarkeitsmatrix nichtlinearer Systeme besteht aus Gradienten von Lie-Ableitungen des Skalarfeldes der Ausgangsabbildung. Alternativ kann man die Zeilen der Beobachtbarkeitsmatrix auch als Lie-Ableitungen eines speziellen Kovektorfeldes, nämlich des Gradienten der Ausgangsabbildung, auffassen. Beim erweiterten Luenberger-Beobachter sind zusätzlich mehrfache Lie-Klammern erforderlich. Erfahrungsgemäß treten dabei deutlich kompliziertere Ausdrücke als beim Reglerentwurf auf. Tatsächlich ist bereits bei moderat komplizierten Systemen die symbolische Berechnung der Beobachterverstärkung zu aufwendig, die Berechnung mit algorithmischem Differenzieren dagegen ohne Probleme durchführbar.
Veröffentlichungen:
- Röbenack, K.; Reinschke, K. J.: A efficient method to compute Lie derivatives and the observability matrix for nonlinear systems. Proc. 2000 International Symposium on Nonlinear Theory and its Applications (NOLTA'2000), Dresden, Sept. 17-21, 2000, 2, 625-628
- Röbenack, K.; Reinschke, K. J.: Nonlinear Observer Design using Automatic Differentiation. In : Corliss, G.; Faure, C.; Griewank, A.; Hascoët, L.; Naumann, U. (Hrsg.), Automatic Differentiation: From Simulation to Optimization, Springer, 2002, Kapitel 15, 137-142
- Röbenack, K.: Computation of the Observer Gain for Extended Luenberger Observers Using Automatic Differentiation. IMA Journal of Mathematical Control and Information, 2004, 21, 33-47
- Röbenack, K.: Computation of High Gain Observers for Nonlinear Systems using Automatic Differentiation. Journal Dynamic Systems, Measurement, and Control, 2005, 127, 160-162
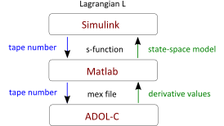
Ausgehend von der Lagrange-Funktion eines mechanischen Systems kann man die Euler-Lagrangeschen Bewegungsgleichungen aufstellen. Dazu sind sind partielle und totale Ableitungen zu bilden. Mit der Kettenregel lässt sich die totale Zeitableitung in partielle Ableitungen zweiter Ordnung auflösen. Wir beschäftigen uns mit der Simulation der Bewegungsgleichungen, ohne diese explizit symbolisch angeben zu müssen. Die Lagrange-Funktion sei in lokalen Koordinaten gegeben und als C++-Code implementiert. ADOL-C stellt eine Reihe von Treibern für die effiziente Berechnung der benötigten ersten und zweiten Ableitungen bereit. Desweiteren steht eine Schnittstelle zu MATLAB zur Verfügung, so dass entsprechende Regelungsaufgaben leicht mit Hilfe von Simulink-Blöcken implementiert werden können. In diesem Rahmen kann das (ggf. eingangsabhängige) Vektorfeld berechnet werden, so dass eine Simulation des Systems unter MATLAB/SIMULINK bequem möglich ist.
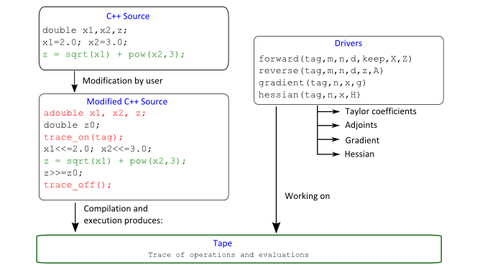
© K. Röbenack (TU Dresden)
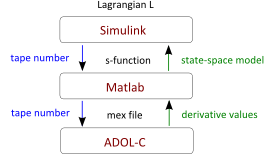
© K. Röbenack (TU Dresden)
Veröffentlichungen:
- Röbenack, K.; Winkler, J.; Knoll, C.: Direct Simulation of mechanical control systems using algorithmic differentiation. In Proc. 56th International Scientific Colloquium, Ilmenau, 2011
- Franke, M.; Zaiczek, T. & Röbenack, K.: Simulation of Nonholonomic Mechanical Systems Using Algorithmic Differentiation. In Proc. 7th Vienna International Conference on Mathematical Modelling (MATHMOD 2012), Wien, 2012.