Forschungsprojekte
Hier führen wir die öffentlich geförderten Projekte an unserem Institut auf.
Inhaltsverzeichnis
- Nichtlinearer Reglerentwurf mit Methoden der algebraischen Geometrie
- Graduiertenkolleg 2430: Interaktive Faser-Elastomer-Verbunde, Teilprojekt 9: Steuerungs- und Regelungskonzepte für die Systemintegration in I-FEV
- STABEEL - Stabilität dezentraler Erzeuger im Elektroenergieversorgungsnetz bei der Erbringung von Systemdienstleistungen
- Nichtlinearer Reglerentwurf mittels Quantorenelimination
- Modellbasierte Steuerung und Regelung des Vertical-Gradient-Freeze-(VGF)- Kristallzüchtungsprozesses mit Hilfe verteiltparametrischer Methoden
Nichtlinearer Reglerentwurf mit Methoden der algebraischen Geometrie
Finanzierung: Deutsche Forschungsgemeinschaft (DFG), Projektnummer 417698841
Laufzeit: 2023 bis 2026
Inhalt:
Vor dem Entwurf einer Regelung stellt sich zunächst die Frage, ob das jeweilige Regelziel mit der an der zu regelnden Anlage gegebenen Aktuierung bzw. vorhandenen Sensorik überhaupt erreicht werden kann. Diese Fragestellung führt auf Konzepte wie die Steuer- und Beobachtbarkeit oder Stabilisierbarkeit. Während derartige Systemeigenschaften für lineare zeitinvariante Systeme klar definiert sind und mit bekannten Kriterien überprüft werden können, gibt es für nichtlineare Systeme zahlreiche Abwandlungen und in der Regel keine verbindliche Möglichkeit, die jeweilige Eigenschaft im Sinne einer sowohl hinreichenden als auch notwendigen Bedingung zu überprüfen. Sind die entsprechenden Voraussetzungen erfüllt, bestehen hinsichtlich der Gestaltung des Regelgesetzes erhebliche Freiheitsgrade. Bei modernen Entwurfsverfahren (z.B. Backstepping) hat man oft die Möglichkeit, nicht nur einzelne reelle Parameter, sondern ganze Funktionen frei zu wählen. Damit ist allerdings auch schon die mathematische Beschreibung der bestehenden Entwurfsfreiheitsgrade nicht einfach. Grundsätzlich lassen sich die bestehenden Spielräume nutzen, um den Regler hinsichtlich der vorgegebenen Anforderungen und gewünschten Eigenschaften auszulegen. Bei einem vorgegebenen Ansatz für einen Regler stellt sich erneut die Frage, ob damit die Regelziele erreicht werden können.
Viele dieser Bedingungen lassen sich durch quantorenbehaftete Aussagen formulieren. Mittels Quantorenelimination überführt man eine Aussage mit Quantoren zu einer äquivalenten quantorenfreien Aussage. Theoretische Grundlage für diese Herangehensweise ist das Taski-Seidenberg-Theorem. Erste Ansätze zur Durchführung der Quantorenelimination wurden schon in der Mitte des letzten Jahrhunderts entwickelt, waren aber aufgrund der algorithmischen Komplexität nicht praktisch einsetzbar. In den letzten Jahrzehnten gab es signifikante Weiterentwicklungen bei den zur Quantorenelimination eingesetzten Algorithmen, sodass mittlerweile auch Software-Werkzeuge für nicht triviale Anwendungen zur Verfügung stehen.
Insbesondere bei der Analyse der Beobachtbarkeit hat sich gezeigt, dass sich dieses Problem durch algebraische Ausdrücke beschreiben lässt. Dies sind quantorenfreie Aussagen, die nur durch Gleichungen, also ohne Ungleichungen, beschrieben werden. Für diese Klasse existieren weit leistungsfähigere Algorithmen. Auf natürliche Weise lässt sich auch ein Beobachter entwerfen, wobei die Funktionen auf algebraischem Wege bestimmt werden. Es ist zu vermuten, dass sich auf ähnliche Art die Steuerbarkeit untersuchen lässt, oder ein Regler konstruiert werden kann.
Damit Systeme mit algebraischen Methoden behandelt werden können, ist eine Beschreibung durch polynomiale Funktionen notwendig. Viele Modelle können in diese Form überführt werden, wobei gegebenenfalls eine Einbettung in einen höherdimensionalen Raum nötig ist. Allerdings gelingt dies beispielsweise bei mechanischen Systemen teils nur in impliziter Form. Für diese Systemklasse sind die bisher entwickelten Methoden zu erweitern.
Graduiertenkolleg 2430: Interaktive Faser-Elastomer-Verbunde, Teilprojekt 9: Steuerungs- und Regelungskonzepte für die Systemintegration in I-FEV
Finanzierung: Deutsche Forschungsgemeinschaft (DFG)
Laufzeit: seit November 2018 bis vsl. Ende 2024
Kooperationspartner:
- TU Dresden, Fakultät Maschinenwesen, Institut für Textilmaschinen und Textile Hochleistungswerkstofftechnik
- TU Dresden, Fakultät Maschinenwesen, Institut für Energietechnik (IET), Professur für Technische Thermodynamik
- TU Dresden, Fakultät Elektrotechnik und Informationstechnik, Institut für Festkörperelektronik
- TU Dresden, Fakultät Maschinenwesen, Institut für Strömungsmechanik
- Leibniz-Institut für Polymerforschung Dresden e.V. (IPF), Institut Theorie der Polymere
- TU Dresden, Fakultät Bauingenieurwesen, Institut für Statik und Dynamik der Tragwerke (ISD)
- TU Dresden, Fakultät Maschinenwesen, Institut für Leichtbau und Kunststofftechnik (ILK), Professur für Funktionsintegrativen Leichtbau
- TU Dresden, Fakultät Maschinenwesen, Institut für Werkstoffwissenschaft (IfWW), Juniorprofessur für Elastomere Werkstoffe
- TU Dresden, Fakultät Maschinenwesen, Institut für Werkstoffwissenschaft (IfWW), Professur für Werkstoffmechanik und Schadensfallanalyse
Inhalt:
- Teilprojekt 9 (2021 - 2024), Mehrvariable robuste Regelung für räumliche Deformationen von I-FEV
- Teilprojekt 9 (2018 - 2023), Steuerungs- und Regelungskonzepte für die Systemintegration in I-FEV
Zur Homepage des Graduiertenkollegs...
STABEEL - Stabilität dezentraler Erzeuger im Elektroenergieversorgungsnetz bei der Erbringung von Systemdienstleistungen
Finanzierung: Deutsche Forschungsgemeinschaft (DFG)
Laufzeit: 2020 bis 2023
Inhalt:
Gegenstand dieses Projektes ist die Erarbeitung anwendungsbezogener Entwurfsrichtlinien zur Bewertung der Stabilität von dezentralen Anlagenregelungen in Elektroenergieversorgungsnetzen. Es wird gemeinsam vom Institut für Regelungs- und Steuerungstheorie (RST) und dem Institut für Elektrische Energieversorgung und Hochspannungstechnik (IEEH) an der TU Dresden mit einer Laufzeit von 3 Jahren durchgeführt.
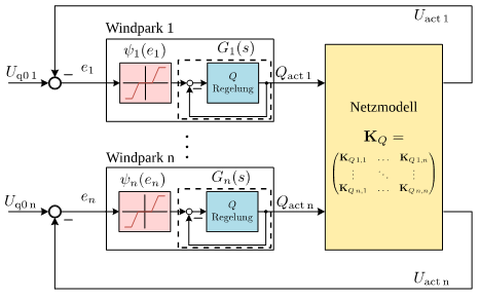
Die Transformation des Elektroenergiesystems im Rahmen der Energiewende erfordert in Hinblick auf die Vielzahl an regelungstechnisch zu erschließenden dezentralen Erzeugungsanlagen (DEAs) anpassungsfähige Betriebsführungskonzepte zur Wahrung der Spannungshaltung. Derzeit greift man z. B. durch Vorgabe zentral optimierter Arbeitspunkte aktiv in den Blindleistungshaushalt von Netzen ein. DEAs unterliegen durch die Quelle der Primärenergie einer technischen Fluktuation und sind zunehmend auch einer ökonomischen Fluktuation ausgesetzt. Sie werden verstärkt in der Direktvermarktung vertrieben, sodass es in Folge der forcierten Fahrplantreue am Übergang zwischen den 15-min-Vermarktungsintervallen zu hohen Leistungsgradienten kommen kann. Die Anlagenregelung sollte demnach Frequenz- und Spannungssprünge, bedingt durch zeitsynchrones Anlagenverhalten, sicher beherrschen können, um unerlaubtes Überschwingen oder Instabilität auszuschließen. Problematisch ist jedoch, dass jede DEA für sich allein regelt und nur die Kenngrößen am eigenen Messpunkt verarbeitet. Die Auswirkung der Gesamtheit aller Stelleingriffe auf das Netz wird seitens der einzelnen DEAs nicht berücksichtigt. Dieser dezentrale Regelungsansatz führt zu theoretisch interessanten und anspruchsvollen regelungstechnischen Fragestellungen.
Wichtig ist dabei zum einen die regelungstheoretisch exakte Formulierung und damit Sicherstellung der Stabilität – auch im Falle von Teilsystemausfällen –, und zum anderen die praktische Anwendbarkeit der Kriterien in Form einfach handhabbarer Richtlinien. Dabei beziehen sich die Untersuchungen auf die Regelung der Blindleistung durch das Q(U)-Verfahren zur Einhaltung gewünschter Spannungsverteilungen.
In diesem Sinne sollen auch Fragen zur Robustheit der Stabilitätsaussagen gegen Parameterunbestimmtheiten und netztypischen Störgrößen behandelt werden. Dazu sollen Methoden entwickelt werden, die es dem Netzbetreiber u. a. erlauben, mit geringem messtechnischen Aufwand eine Bewertung der aktuellen Stabilitätsreserve unter voller Berücksichtigung des Parameterraums in einem Netzgebiet durchzuführen.
Des Weiteren sollen im Projekt Verfahren zur Detektion und Isolation von fehlerhaften Anlagenregelungen oder veränderten Reglerstrukturen entwickelt und erprobt werden. Mit diesen vielschichtigen Ansätzen wird versucht, sich der Problemstellung theoretisch anspruchsvoll (Residuengenerator oder Mustererkennung) als auch mit einer praktischen Fallback-Lösung (Sensorbasis) zu nähern. Die Erkenntnisse können als Grundlage für künftige Forschungsvorhaben im Bereich der automatisierten Netzbetriebsführung dienen.
Die im Rahmen des Projektes gewonnenen Erkenntnisse werden an einem physikalisch am IEEH vorhandenen leistungsfähigen dynamischen Netzwerkmodell praktisch erprobt.
Nichtlinearer Reglerentwurf mittels Quantorenelimination
Finanzierung: Deutsche Forschungsgemeinschaft (DFG), Projekt RO 2427/5-1
Laufzeit: 2019 bis 2022
Inhalt:
Bei etlichen modernen Entwurfsverfahren für Regelungen (z.B. Backstepping) bestehen erhebliche Freiheiten zur konkreten Gestaltung des Regelgesetzes. Diese Spielräume beim Reglerentwurf lassen sich prinzipiell nutzen, um den Regler hinsichtlich der vorgegebenen Anforderungen und gewünschten Eigenschaften auszulegen. Tatsächlich ist allerdings schon die exakte mathematische Beschreibung der bestehenden Entwurfsfreiheitsgrade nicht einfach. Auch standen diese Entwurfsfreiheiten, die sehr individuelle Anpassungen erlauben, bisher einem automatisierten Entwurf, wie er beispielsweise bei der exakten Eingangs-Ausgangs-Linearisierung möglich ist, entgegen.
Das wichtigste Entwurfsziel einer Regelung ist die Stabilität des geschlossenen Regelkreises. Bei nichtlinearen System werden Stabilitätsforderungen an den geschlossenen Regelkreis in aller Regel über Ljapunov-Ansätze formuliert, aus denen man bisher durch geschickte Abschätzungen den Regler bzw. die Reglerparameter ermittelt hat. Durch diese Abschätzungen wird man allerdings oft auf konservativ ausgelegte Regler geführt.
Die über Ljapunov-Ansaätze formulierten Stabilitätsbedingungen beruhen auf quantorenbehafteten (pränexen) Aussagen. Mittels Quantorenelimination (QE) überführt man eine Aussage mit Quantoren zu einer äquivalenten quantorenfreien Aussage. Theoretische Grundlage für diese Herangehensweise ist das Taski-Seidenberg-Theorem. Erste Ansätze zur Durchführung der Quantorenelimination wurden schon in der Mitte des letzten Jahrhunderts entwickelt, waren aber aufgrund der algorithmischen Komplexität nicht praktisch einsetzbar. In den letzten Jahrzehnten gab es signifikante Weiterentwicklungen bei den zur Quantorenelimination eingesetzten Algorithmen, so dass mittlerweile auch Software-Werkzeuge für nicht triviale Anwendungen zur Verfügung stehen.
Methoden der Quantorenelimination fanden in der Regelungstechnik bisher nur vereinzelt, dann auch nur bei sehr einfachen, fast ausschließlich linearen Systemen, Anwendung.
Das Ziel des Forschungsprojekts besteht darin, typische Entwurfsprobleme bei der Regelung nichtlinearer Systeme mittels Quantorenelimination zu lösen. Der Übergang von einer quantorenbehafteten Stabilitätsformulierung zur konkreten Reglerauslegung soll damit algorithmisiert werden.
Modellbasierte Steuerung und Regelung des Vertical-Gradient-Freeze-(VGF)- Kristallzüchtungsprozesses mit Hilfe verteiltparametrischer Methoden
Finanzierung: Deutsche Forschungsgemeinschaft (DFG), Projekt WI 4412/1-1
Laufzeit: seit März 2016
Kooperationspartner:
- Leibniz-Institut für Kristallzüchtung (IKZ) im Forschungsverbund Berlin e.V., Dr. Chr. Frank-Rotsch
- UMIT - Private Universität für Gesundheitswissenschaften, Medizinische Informatik und Technik GmbH, Prof. Dr.-Ing. Frank Woittennek
Inhalt: Ein sehr wichtiger Prozess zur Herstellung einkristalliner Werkstoffe ist das sogenannte Vertical-Gradient-Freeze (VGF) Verfahren. Bei diesem wird polykristallines Ausgangsmaterial in einem senkrecht stehenden Tiegel aufgeschmolzen und anschließend langsam von einem am Boden befindlichen Keimkristall aus erstarrt. Dazu wird ein Temperaturfeld so gesteuert, dass die Schmelzpunktisotherme langsam nach oben über die im Tiegel befindliche Schmelze wandert. Die hierfür nötigen Stelleingriffe werden bspw. durch Widerstandsheizer realisiert, die um den Tiegel angeordnet sind. Um den Prozesses zu beherrschen, ist es erforderlich, Informationen über den momentanen Zustand des Systems in Echtzeit zu erhalten. Insbesondere die Kristallisationsrate des Kristalls ist von Interesse. Diese lässt sich jedoch nicht direkt erfassen. Dies hängt mit den hohen Temperaturen, der Reaktivität der verwendeten Materialien und den Reinheitsanforderungen zusammen, die eine Platzierung von Messeinrichtungen innerhalb des Tiegels verbieten. Lediglich die Temperaturen der Heizelemente stehen als Messinformation zur Verfügung. Damit ist es derzeit ausgeschlossen, mittels einer Rückführung (Regelung) direkt auf den Prozess einzuwirken, er wird nur gesteuert ?black box? betrieben. Aus regelungstheoretischer Sicht handelt es sich bei dem Prozess um einen typischen Vertreter aus der Klasse der sog. verteiltparametrischen Systeme mit konzentriertem Stelleingriff (Heizer) und teilweise freiem Rand (Phasengrenze Schmelze-Kristall).
Gegenstand des Projektes ist die theoretische und praktische Entwicklung von Methoden zur Etablierung einer Regelung des Prozesses. Dies beinhaltet auch Verfahren zur Rekonstruktion des Systemzustandes aus den zur Verfügung stehenden oder neu einzuführenden Messgrößen. Hierzu sollen verteiltparametrische Methoden, die am Institut für Regelungs- und Steuerungstheorie (TU Dresden) seit vielen Jahren untersucht und maßgeblich entwickelt wurden, genutzt und weiterentwickelt werden. Der wissenschaftliche Erkenntnisgewinn liegt hier vor allem in der Etablierung von theoretischen Verfahren zur Realisierung einer Regelung für diese Modellklasse. Bislang lag der Fokus weitgehend auf der Steuerung und Parameteridentifikation. Dies ist gepaart mit sehr umfangreichen Arbeiten zur Modellbildung am Institut für Kristallzüchtung Berlin (IKZ). Diese Modelle werden zum einen für den eigentlichen Regler- und Beobachterentwurf benötigt, als auch zur Validierung der entworfenen Regelungskonzepte, um so den Experimentalaufwand zu reduzieren. Die Herausforderung ist dabei, mathematische Modelle des Prozesses aufzustellen, die für die Regelungsaufgabe hinreichend genau, echtzeitfähig und für die vorgesehenen regelungstheoretischen Methoden strukturell geeignet sind. Die entwickelten Verfahren sollen eingebettet in einem theoretisch anspruchsvollen Rahmen streng auf die praktische Verwertbarkeit entwickelt und letztendlich am realen Prozess am IKZ getestet werden.
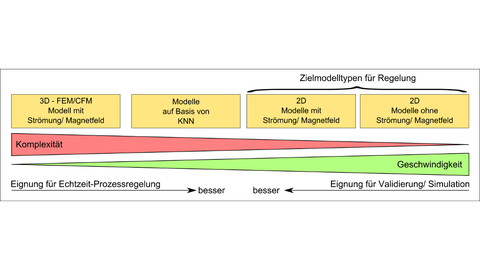
Vergleich unterschiedlicher Modelltypen und deren Eigenschaften für die Regelung.