SPP1713 - Stark gekoppelte thermo-chemische und thermo-mechanische Zustände in Angewandten Materialien

Modellierung des stark gekoppelten magneto-mechanischen Verhaltens magnetosensitiver Elastomere

Funktionalisierte Polymere stellen eine neue und interessante Klasse von aktiven Werkstoffen dar. Sie besitzen eine lokal heterogene Materialstruktur und ihr Verhalten weist eine starke Kopplung mechanischer und äußerer Felder auf. Bedingt durch den Einfluss der externen Felder entstehen Wechselwirkungen innerhalb sowie zwischen einzelnen Materialphasen, die zu Veränderungen der Mikrostruktur führen können. Zu der genannten Werkstoffklasse zählen auch die im Teilprojekt P3 des Schwerpunktprogramms SPP 1713 betrachteten magnetosensitiven Elastomere. Sie weisen magnetfeldabhängige mechanische Steifigkeiten sowie magnetisch induzierbare Verformungen und Aktorspannungen auf und kommen daher in zahlreichen Bereichen der Technik, zum Beispiel in Aktoren, Sensoren, Mikrorobotern und -pumpen oder -ventilen, zum Einsatz. Magnetosensitive Elastomere bestehen aus mikrometergroßen magnetisierbaren Partikeln, die in eine weiche Elastomermatrix eingebettet sind. Abhängig vom jeweiligen Vernetzungsgrad ermöglichen die elastisch verformbaren Polymerketten eine Bewegung der Partikel innerhalb des Netzwerkes. Bei hinreichend großen magnetischen Feldern können sich die Partikel auch irreversibel verschieben. In der Folge kommt es zu Veränderungen der Mikrostruktur, die das gekoppelte magneto-mechanische Verhalten entscheidend beeinflussen. Das Ziel dieses Projekts besteht in der Vorhersage des makroskopischen, gekoppelten magneto-mechanischen Verhaltens von magnetosensitiven Elastomeren. Dafür sind an der Professur für Nichtlineare Festkörpermechanik folgende Aufgaben zu bearbeiten:

Modellierung des gekoppelten magneto-mechanischen Verhaltens magnetosensitiver Elastomere bei großen Deformationen
Entwicklung eines effizienten und robusten Lösungsschemas zur numerischen Simulation magnetosensitiver Elastomere mithilfe der Finite-Elemente Methode
Erarbeitung eines Frameworks zur magneto-mechanischen Homogenisierung bei großen Deformationen
Vorhersage des effektiven Materialverhaltens magnetosensitiver Elastomere auf der Basis verschiedener idealisierter und realitätsnaher Mikrostrukturen
Entwicklung eines Phasenfeld- bzw. Gradientenmodells zur Beschreibung der Mikrostrukturevolution magnetosensitiver Elastomere
Vergleich der generierten Ergebnisse mit experimentellen Daten sowie in der Literatur verfügbaren Arbeiten

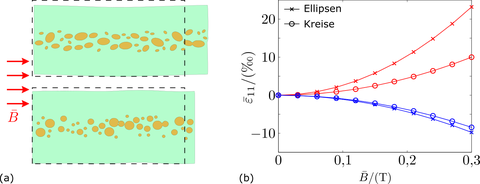
SPP1713 — Magnetostriktiver Effekt am Beispiel kettenförmiger Mikrostrukturen mit ellipsen- und kreisförmigen Einschlüssen: (a) überhöhte Darstellung der verformten Mikrostrukturen; (b) Darstellung der effektiven Verzerrung in Abhängigkeit der effektiven Flussdichte (blaue Linien zeigen den selben Effekt bei Vorgabe eines Feldes in vertikale Richtung)

Projektmitarbeiter

Dipl.-Ing. Philipp Metsch

E-Mail senden

Kontaktinformationen

Professur für Numerische und Experimentelle Festkörpermechanik

work

Besuchsadresse:

MAR, Zimmer 053 Marschnerstraße 30

01307 Dresden

Zeige Karte von diesem Ort.

work Tel.
fax Fax: +49 351 463-37061

Projektleitung

Inhaber der Professur für Numerische und Experimentelle Festkörpermechanik

Prof. Dr.-Ing. habil. Markus Kästner

E-Mail senden

Kontaktinformationen

Professur für Numerische und Experimentelle Festkörpermechanik

work

Besuchsadresse:

Zeunerbau, Zimmer 352 George-Bähr-Straße 3c

01069 Dresden

Zeige Karte von diesem Ort.

work Tel.
fax Fax: +49 351 463-37061

Kooperationen

DFG Schwerpunktprogramm SPP 1713
PD Dr. Marina Grenzer, Leibniz Institut für Polymerforschung, Dresden
Dr. Dirk Romeis, Leibniz Institut für Polymerforschung, Dresden

Publikationen

Artikel in begutachteten Zeitschriften

P. Metsch, D. Romeis, K. A. Kalina, A. Raßloff, M. Sphiannikova, M. Kästner
Magneto-Mechanical Coupling in Magneto-Active Elastomers
Materials 14, S. 434, 2021. [DOI]
P. Metsch, H. Schmidt, D. Sindersberger, K. A. Kalina, J. Brummund, G. K. Auernhammer, G. J. Monkman, M. Kästner
Field-induced interactions in magneto-active elastomers - A comparison of experiments and simulations
Smart Materials and Structures 29, S. 085026, 2020. [DOI]
P. Metsch, K.A. Kalina, J. Brummund, M. Kästner
Two- and three-dimensional modeling approaches in magneto-mechanics: a quantitative comparison
Archive of Applied Mechanics 89, S. 47-62, 2019. [DOI]
D. Romeis, P. Metsch, M. Kästner, M. Saphiannikova
Theoretical Models for Magneto-Sensitive Elastomers: A Comparison between Continuum and Dipole Approaches
Physical Review E 95, S. 042501, 2017. [DOI]
K. A. Kalina, P. Metsch, M. Kästner,
Microscale modeling and simulation of magnetorheological elastomers at finite strains: A study on the influence of mechanical preloads
International Journal of Solids and Structures, 2016. [DOI]
P. Metsch, K. A. Kalina, C. Spieler, M. Kästner,
A numerical study on magnetostrictive phenomena in magnetorheological elastomers
Computational Materials Science 124, S. 364-374, 2016. [DOI]
M. Kästner, P. Metsch, R. de Borst
Isogeometric analysis of the Cahn-Hilliard equation - a convergence study
Journal of Computational Physics 305, S. 360-371, 2016. [URL]

Proceedings

P. Metsch, H. Schmidt, K. A. Kalina, J. Brummund, G. G. Auernhammer, M. Kästner
Particle Interactions in Magneto-Active Elastomers: Experiments and Simulations
Proceedings in Applied Mathematics and Mechanics 20, S. e202000277, 2021. [DOI]
P. Metsch, K. A. Kalina, J. Brummund, M. Kästner
A quantitative comparison of two-and three-dimensional modeling approaches for magnetorheological elastomers
Proceedings in Applied Mathematics and Mechanics 18, S. e201800179, 2018. [DOI]
P. Metsch, D. Romeis, M. Saphiannikova, M. Kästner
Modeling and simulation of magnetorheological elastomers: A comparison of continuum and dipole approaches
Proceedings in Applied Mathematics and Mechanics 17, S. 527-528, 2017. [DOI]

Konferenzbeiträge

P. Metsch, K. A. Kalina, Jörg Brummund, G. K. Auernhammer, M. Kästner
Microscale analysis of interactions in magnetorheological elastomers
89^th Annual Meeting of the International Association of Applied Mathematics and Mechanics, München, 2018
P. Metsch, D. Romeis, M. Saphiannikova, M. Kästner
Modeling and simulation of magnetorheological elastomers: A comparison of continuum and dipole approaches
88^th Annual Meeting of the International Association of Applied Mathematics and Mechanics, Weimar, 2017
P. Metsch, K. A. Kalina, M. Kästner
Modeling and simulation of coupling effects in magnetorheological elastomers
Materials Science and Engineering Congress, Darmstadt, 2016
P. Metsch, K. A. Kalina, C. Lux, M. Kästner
Modeling and simulation of magnetorheological elastomers at finite strains
15^th European Mechanics of Materials Conference, Brüssel, 2016
P. Metsch, K. Kalina, C. Spieler, D. Romeis, M. Saphiannikova, M. Kästner
Modeling and simulation of magnetostrictive phenomena in magnetorheological elastomers
Joint Annual Meeting of DMV and GAMM, Braunschweig, 2016 [Abstract]
P. Metsch, C. Spieler, M. Kästner
Magnetostriction of magnetorheological elastomers - finite element modeling and simulation
7^th International Symposium on Design, Modelling and Experiments of Advanced Structures and Smart Systems, Radebeul, 2015 [Abstract]
P. Metsch, C. Spieler, M. Kästner
Microscopic modeling and finite element simulation of magnetorheological elastomers
86^th Annual Meeting of the International Association of Applied Mathematics and Mechanics, Lecce, 2015 [Abstract]
P. Metsch, C. Spieler, M. Kästner
Multiscale Finite Element Modeling of Magnetoactive Materials
79^th Annual Meeting of the DPG and DPG Spring Meeting, Berlin, 2015 [Abstract]
P. Metsch, M. Kästner
Isogeometric analysis of the Cahn-Hilliard phase-field model – A convergence study
2^nd GAMM Seminar on Phase-Field-Modelling, Siegen, 2015 [Abstract]