Modellierung und Simulation des statischen und dynamischen Verhaltens vorgespannter Fugen in Werkzeugmaschinen mittels Relativbettungselementen
| Laufzeit: | 01/2016 - 06/2017 |
| Finanzierung: | DFG |
| Bearbeiter: | Dr.-Ing. Holger Rudolph |
Zielstellung
Die Finite Elemente Methode (FEM) ist ein wichtiges und nicht mehr wegzudenkendes Hilfsmittel zur Simulation des statischen und dynamischen Verhaltens von Werkzeugmaschinen. Die in der FEM eingesetzten Elemente verwenden Ansatzfunktionen zur Approximation ihres physikalischen Verhaltens. Typischerweise kommen dabei lineare oder auch höherpolynomische Funktionen zur Anwendung. Die Verwendung von linearen Elementen hat zwar den Vorteil der numerischen Einfachheit, jedoch den Nachteil, dass für eine ausreichende Modellgüte viele Elemente erforderlich sind. Demgegenüber kann mit wenigen Elementen höherer Ordnung ebenfalls ein hinreichend genaues Modell erstellt werden. Die Modellierung von elastischen Fugen (z. B. an Verbindungsstellen von Bauteilen und Baugruppen) stellt in diesem Zusammenhang bislang ein größeres Problem dar. Neben der eigentlichen Kontaktstellenbeschreibung beeinflussen hier auch technologisch bedingte Größen, wie die Oberflächenrauheit und die Formabweichungen in der Kontaktzone, die Charakteristik – also in erster Linie die Steifigkeit und das Dämpfungsvermögen – derartiger Verbindungsstellen. Die heute hierbei verwendeten Modelle sind nur begrenzt für eine rechnerische Modal- und Frequenzganganalyse von Werkzeugmaschinen brauchbar.
Dieses Forschungsvorhaben will daher einen Ansatz zur Modellierung von elastischen Fugen schaffen und anwenden, welcher die bisher übliche, feine Vernetzung an den Fugenflächen überflüssig macht und zudem mit höherpolynomischen finiten Elementen kompatibel ist. Angesichts der weit auseinanderliegenden Charakteristika bei den existierenden Modellvorstellungen aus der Literatur, den Unsicherheiten bei einer Vorab-Bestimmung der Einflussgrößen auf die resultierenden Steifigkeiten sowie der im Werkzeugmaschinenbau üblicherweise deutlich größeren Vorspannung gegenüber den Prozesslasten erscheint eine Linearisierung der Fugenmodelle in jedem Fall angemessen.
Das Ziel der ersten Projektphase liegt im experimentellen Nachweis einer hinreichenden Zulässigkeit zur modellseitigen Linearisierung von Steifigkeit und Dämpfung in verschiedenen Arbeitspunkten vorgespannter Fugen.
Lösungsweg
Der experimentelle Nachweis wird an einer Reihe von beispielhaften Versuchsbaugruppen mittels statischer und dynamischer Analysen geführt. Ausgangspunkt ist in jedem Fall die messtechnische Ermittlung der Oberflächengüte der Probekörper und der Flächenpressung in der Kontaktzone bei verschiedenen Vorspannungen. Bild 1 zeigt hierzu exemplarisch die Pressungsverteilung an nominell planaren Kontaktflächen, die mit unterschiedlichen technologischen Verfahren gefertigt wurden. In den vorliegenden Fällen sind die plangedrehten Flächen leicht konkav und die geschliffenen Flächen (ohne Ausfeuern) leicht konvex. Hingegen ist die Ebenheitsabweichung bei den gefrästen und den geschliffenen Oberflächen (mit Ausfeuern) weitgehend gleichmäßig über den Flächen verteilt.
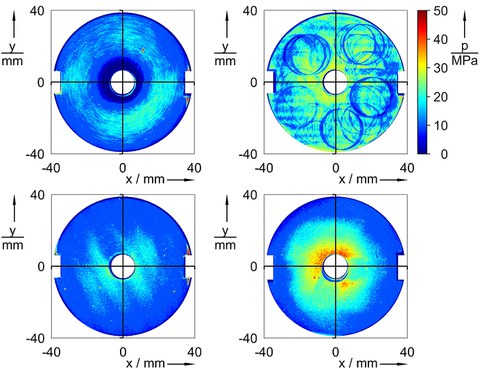
Bild 1: Flächenpressung in der Kontaktzone bei Schraubenmoment 100 Nm, Fläche plangedreht (links oben), gefräst (rechts oben), geschliffen (unten)
Parallel zu den experimentellen Untersuchungen werden korrespondierende FEM-Modelle der Versuchsbaugruppen erstellt. Ein Hauptaugenmerk liegt hierbei auf der Erstellung regulärer und kollokierter Knotennetze, um auch unterschiedliche Modellansätze zur Beschreibung von Fugen realisieren zu können. Die resultierende Fugensteifigkeit wird über einen nichtlinearen Optimierungsalgorithmus am FEM‑Modell anhand der Schwingungsformen identifiziert.
Ergebnisse
Erste Ergebnisse liegen für zwei grundsätzliche Modellierungsansätze vor - diskrete Federelemente und flächige Kontaktelemente. Beide Ansätze sind mit diversen Parametrisierungen - hinsichtlich der Steifigkeitsverteilung - bzw. Berechnungsoptionen – hinsichtlich der Kontaktalgorithmen - analysiert worden. Das Bild 2 zeigt hierzu die Abweichung der Eigenfrequenzen für die einzelnen Modellvarianten in Relation zu den Messergebnissen für die kleinste in der Testreihe auftretende Fugensteifigkeit an den geschliffenen, konvexen Oberflächen. Infolge der Geometrie der Probekörper treten die Biegeschwingungsformen als Paare mit geringfügig unterschiedlichen Eigenfrequenzen auf. Die Balken im Diagramm stellen die mittleren Abweichungen dieser Frequenzen dar, die Fehlerbalken markieren die Spannweite zwischen den Eigenfrequenzpaaren.
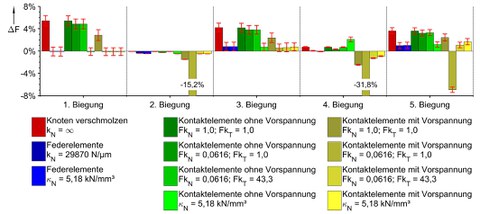
Bild 2: Relative Abweichung der Biege-Eigenfrequenzen zwischen Messung und Modellen mit verschiedenen Fugenbeschreibungen für die konvex geschliffenen Oberflächen bei Schraubenmoment 25 Nm
