Research Field "Computational Methods"
Many applications of Finite Element Methods or eXtended Finite Element Methods lead to inaccurate results if standard elements are used or are not robust. At the institute computational methods are developed to stabilise the XFEM, to avoid locking effects and to improve the efficiency of finite element technologies. As a result these computational methods extend the field of applications of finite elements. Another research field is error controlled adaptive finite element methods that can be used to obtain an estimation of the accuracy of a finite element or extended finite element solution and to adapt the discretisation as well as the model to the desired accuracy.
Research Projects
Contact:
Stefan Löhnert
Abstract:
Using the XFEM for the simulation of cracks or heterogeneities due to the position of the discontinuity and due to the desired enrichment function it is possible that near linear dependencies may occur between some of the degrees of freedom. These near linear dependencies in general lead to very bad conditioning of the resulting equation system which can cause significant numerical difficulties. In this project stabilisation techniques are developed to avoid near linear dependencies and to improve the conditioning of the resulting equation system without loosing accuracy. The method is based on a singular value decomposition of the element stiffness matrix of elements of which all nodes are enriched. All singular modes with a singular value below a given tolerance are stabilised. Physically or numerically reasonable zero singular modes are excluded from the stabilisation. Due to the fact that for most applications the number of elements of which all the nodes are enriched is rather low, the additional numerical effort is low as well. This type of regularisation reduces the condition number of the resulting equation system by multiple orders of magnitude.
Contact:
Stefan Löhnert
Abstract:
For nearly incompressible materials such as rubber or many types of polymers as well as for metals in their plastic regime lower order finite elements based on Lagrangian shape functions show locking effects. Similarly also for XFEM elements locking may occur. One option to reduce locking or to avoid it completely is to apply mixed formulations. These methods have proven to be good for finite elements. In this project mixed formulations are extended to the XFEM. Here, different enrichments can be employed as they are typically applied to fracture simulations in linear elastic fracture mechanics or to simulations of heterogeneities under small or finite deformations. Using these mixed XFEM formulations locking can be avoided and the convergence properties become independent of the compressibility of the material.
Contact:
Stefan Löhnert, Jian Sun, Rohan Patel, Tengfei Lyu
Abstract:
Applying realistic boundary conditions to a body with a distribution of cracks, some of the cracks may close. If these cracks are simulated with the XFEM, without consideration of additional constraints unphysical overlaps might occur. To avoid this, contact formulations are necessary. In contrast to well established contact formulations for classical finite elements, when employing the XFEM the additional difficulty of an implicit description of the crack surfaces, e.g. by means of level sets arises. Then, the contact constraint can be evaluated in an implicit manner as well by the calculation of the displacements along the crack surface on the desired crack face. Since displacements tangential to the crack surface are possible as well, crack face contact may occur between different elements which needs to be considered in the implementation. For the evaluation of and compliance with the contact constraint classical master-slave concepts in combination with penalty of Lagrange multiplier methods can be employed.
Abstract:
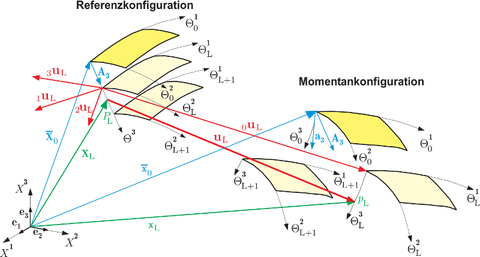
This research work introduces, in a continuum-mechanical approach, the formulation of a mechanical model in connection with the transformation into a shell element using the finite element method for the simulation of the load-bearing behavior of laminated shell structures thereby considering delamination as a type of damage. This multi-layer model is based upon the development of a geometrically nonlinear surface-related shell theory with shear-elastic behavior and variable thickness, beginning with the complete kinematics of a multi-director theory. The surface relationship ensures a mechanical modelling which is adaptable for contact problems. A linear-elastic orthotropic material law, whose three-dimensionality is not restricted by the shell formulation, applies within the layers. The main focus of the thesis is on the development of a layer-bond model that can be adjusted for different materials. The debonding of layers – called delamination – is described by a simple stress criterion. Delamination is discretely taken into account by modifying the kinematic conditions. A contact model, called “inner contact”, which can be used to account for adhesion between layers, has been developed to describe the load-bearing behavior after delamination has occurred. The present shell model is restricted to elastic material behavior and can preferably be applied to such problems where small relative displacements are expected. The environment, in which this research has been conducted, established the primary of application area, which is the simulation of shell structures within a strengthening layer comprised of textile-reinforced concrete.
References:
Dissertation Jan Matheas, 2005, TU Dresden
DFG (Deutsche Forschungsgemeinschaft), Sonderforschungsbereich 528: Textile Bewehrungen zur bautechnischen Verstärkung und Instandsetzung
Teilprojekt C2: Verbundverhalten flächiger Verstärkungen
Verformte und verformte geschlitzte Kreisringplatte bei maximaler Last
Abstract:
Das Pojekt ist auf die theoretischen und numerischen Aspekte der Herleitung oberflächenorientierter Schalentheorien und Schalenelemente bzw. Volumen-Schalenelemente sowie ihrer Umsetzungen in ein leistungsstarkes Finite-Element-Programmpaket gerichtet. Kern der Arbeiten ist die Verwendung der Kontaktmechanik zur Beschreibung des Schichtenverbundes insbesondere im Zusammenhang mit oberflächenorientierten Mehrschichten-Multidirektor-Schalenelementen. Im Vordergrund steht die Ermittlung von Kontaktspannungszustand und Delamination, zum einen zwischen Grundmaterial und Verstärkung, zum anderen in beliebigen Flächen der Schichtengrenzen innerhalb der Verstärkung.
Weitere Informationen sind der Detailbeschreibung zu entnehmen.
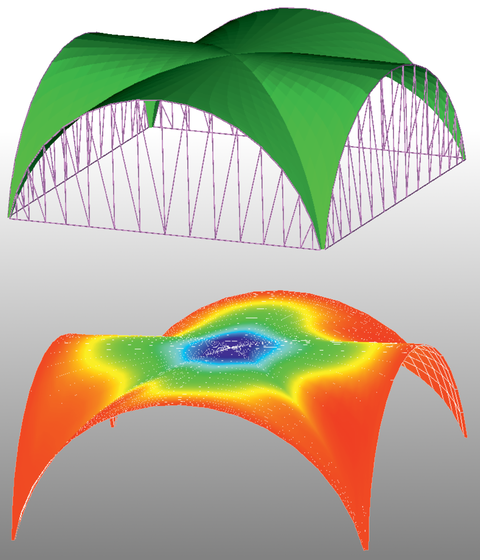
Verformungsberechnung eines Schalentragwerkes in Form eines Kreuzgewölbes mit quadratischer Grundfläche
Abstract:
DREFES ist eine Adaption des Programms FEABL, das ursprünglich am Department of Aeronautics and Astronautics des Massachusetts Institute of Technology (USA) entwickelt wurde. Es handelt sich um eine Software, die Finite-Elemente-Berechnungen ermöglicht. Die Simulationssoftware ist im Laufe der Zeit u.a. um diverse Schalen-Elemente, insbesondere um oberflächenorientierte Mehrschichten-Multidirektor-Schalenelemente erweitert worden. Sie kann zur numerischen Simulation von textilbetonverstärkten flächigen Bauteilen verwendet werden, wobei Delamination und Kontakt in der Simulation erfasst werden können.
Weitere Informationen sind der Detailbeschreibung zu entnehmen.
link to research field "Damage and Fracture Mechanics"
link to research field "Multiphysical Material Modelling on Multiple Scales"