Research Projects
Here we list the publicly funded projects at our Institute.
Table of contents
- Nonlinear Controller Design using Methods from Algebraic Geometry
- Research Training Group 2430: Interactive fiber-elastomer composites, sub-project 9: Control and regulation concepts for system integration in I-FEV
- STABEEL - Stability of decentralized generators in the electrical power supply grid in the provision of system services
- Nonlinear controller design using quantifier elimination
- Model-based control and regulation of the vertical gradient freeze (VGF) crystal growth process using distribution parametric methods
Nonlinear Controller Design using Methods from Algebraic Geometry
Funding: German Research Foundation (DFG)
Duration: since 2023-2026
Content
Control theory asks for the ability to stabilize systems using given control inputs and measurable outputs only, while meeting design goals. This leads to whether the system is controllable or observable. These properties are well-defined and easy to test for linear systems. However, there is a multitude of definitions for nonlinear systems and. Furthermore, the criteria are often not necessary and sufficient or are
extremely difficult to test. If the conditions are fulfilled, there is a large degree of freedom for the controller design. That is, there is not only a parameter space but entire functions can be chosen freely. While this complicated the description, the degrees of freedom can be used to shape the controller to meet specified goals.
Many criteria can be formulated as quantified expressions. These can be transformed into equivalent quantifier free formulas by the Tarski-Seidenberg theorem. There exist algorithms for this transformation, which are computationally very complex. Since significant improvements were made in recent years, there are software tools that can handle nontrivial examples, now.
The problem of nonlinear observability can be formulated by algebraic means, that is, quantifier free formulas without inequalities. For these class there exists much more efficient tools. Furthermore, observers can be constructed mostly in an automatic ways based on these methods. This raises the natural question, if this method can be adopted to controllability or controller design.
To be able to handle systems with these algebraic approaches, these have to be formulated using polynomials. Many systems can be transformed to meet this requirement, possibly by embedding into higher dimensional spaces. Others may be represented in implicit polynomial form. The goal is to extend the analysis and synthesis methods for this larger class.
Research Training Group 2430: Interactive fiber-elastomer composites, sub-project 9: Control and regulation concepts for system integration in I-FEV
Funding: German Research Foundation (DFG)
Duration: since November 2018 until probably the end of 2024
Cooperation partners:
- TU Dresden, Faculty of Mechanical Science and Engineering, Institute of Textile Machinery and High Performance Material Technology
- TU Dresden, Faculty of Mechanical Science and Engineering, Institute of Power Engineering (IET), Chair of Thermodynamics
- TU Dresden, Faculty of Electrical and Computer Engineering, Institute of Solid State Electronics
- TU Dresden, Faculty of Mechanical Science and Engineering, Institute of Fluid Mechanics
- Leibniz Institute of Polymer Research Dresden e.V. (IPF), Institute Theory of Polymers
- TU Dresden, Faculty of Civil Engineering ,Institute of Structural Analysis (ISD)
- TU Dresden, Faculty of Mechanical Science and Engineering, Institute of Lightweight Engineering and Polymer Technology (ILK), Chair of Function-integrative Lightweight Engineering
- TU Dresden, Faculty of Mechanical Science and Engineering, Institute of Materials Science (IfWW), Junior Professorship for Elastomeric Materials
- TU Dresden, Faculty of Mechanical Science and Engineering, Institute of Materials Science (IfWW), Chair of Mechanics of Materials and Failure Analysis
Contents:
- Subproject 9 (2021 - 2024), Multi-variable robust control for spatial deformations of I-FEV
- Subproject 9 (2018- 2023), Control and regulation concepts for system integration in I-FEV
To the homepage of the research training group...
STABEEL - Stability of decentralized generators in the electrical power supply grid in the provision of system services
Funding: German Research Foundation (DFG)
Duration: 2020 to 2023
Content:
The subject of this project is the development of application-oriented design guidelines for evaluating the stability of decentralized plant controls in electrical power supply networks. It is carried out jointly by the Institute of Control Theory (RST) and the Institute of Electrical Power Supply and High Voltage Engineering (IEEH) at TU Dresden with a duration of 3 years.
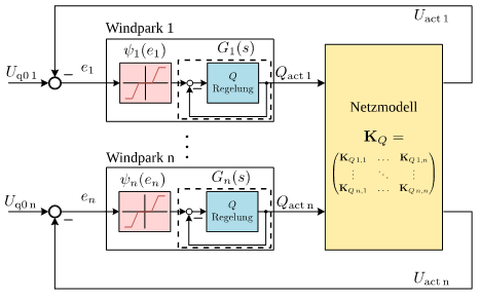
The transformation of the electrical energy system as part of the energy transition requires adaptable operational management concepts to maintain voltage stability in view of the large number of decentralized generation plants (DEAs) to be developed in terms of control technology. Currently, for example, centrally optimized operating points are used to actively intervene in the reactive power balance of grids. Due to the source of primary energy, DEAs are subject to technical fluctuation and are also increasingly exposed to economic fluctuation. They are increasingly being sold in direct marketing, so that high power gradients can occur at the transition between the 15-minute marketing intervals as a result of the forced schedule adherence. The system control should therefore be able to reliably control frequency and voltage jumps caused by time-synchronous system behavior in order to rule out unauthorized overshooting or instability. However, it is problematic that each DEA regulates on its own and only processes the parameters at its own measuring point. The effect of all control interventions on the grid is not taken into account by the individual DEAs. This decentralized control approach leads to theoretically interesting and challenging control issues.
On the one hand, it is important to formulate the control theory precisely and thus ensure stability - even in the event of subsystem failures - and on the other hand, the practical applicability of the criteria in the form of easy-to-use guidelines. The investigations relate to the control of reactive power using the Q(U) method to maintain the desired voltage distributions.
In this sense, questions regarding the robustness of the stability statements against parameter indeterminacies and network-typical disturbance variables will also be addressed. To this end, methods are to be developed which, among other things, allow the grid operator to carry out an assessment of the current stability reserve with little metrological effort, taking full account of the parameter space in a grid area.
The project also aims to develop and test methods for detecting and isolating faulty system controls or modified controller structures. With these multi-layered approaches, an attempt will be made to approach the problem in a theoretically sophisticated way (residual generator or pattern recognition) as well as with a practical fallback solution (sensor basis). The findings can serve as a basis for future research projects in the field of automated grid operation management.
The knowledge gained in the project will be tested in practice on a powerful dynamic network model physically available at the IEEH.
Nonlinear controller design using quantifier elimination
Funding: German Research Foundation (DFG), project RO 2427/5-1
Duration: 2019 to 2022
Content:
In a number of modern control design methods (e.g. backstepping), there is considerable freedom in the concrete design of the control law. In principle, this freedom in controller design can be used to design the controller with regard to the specified requirements and desired properties. However, even the exact mathematical description of the existing degrees of design freedom is not easy. In addition, these design freedoms, which allow very individual adjustments, have so far stood in the way of automated design, as is possible with exact input-output linearization, for example.
The most important design objective of a control system is the stability of the closed control loop. In the case of non-linear systems, stability requirements for the closed control loop are usually formulated using Lyapunov approaches, from which the controller or controller parameters have so far been determined using clever estimations. However, these estimates often lead to conservatively designed controllers.
The stability conditions formulated using Lyapunov approaches are based on quantifier-related (prenex) statements. Quantifier elimination (QE) is used to convert a statement with quantifiers into an equivalent quantifier-free statement. The theoretical basis for this approach is the Taski-Seidenberg theorem. The first approaches for performing quantifier elimination were developed in the middle of the last century, but were not practically applicable due to their algorithmic complexity. In recent decades, there have been significant developments in the algorithms used for quantifier elimination, so that software tools are now also available for non-trivial applications.
Quantifier elimination methods have so far only been used sporadically in control engineering, and then only for very simple, almost exclusively linear systems.
The aim of the research project is to solve typical design problems in the control of non-linear systems by means of quantifier elimination. The aim is to algorithmize the transition from a quantifier-based stability formulation to the actual controller design.
Model-based control and regulation of the vertical gradient freeze (VGF) crystal growth process using distribution parametric methods
Funding: German Research Foundation (DFG), Project WI 4412/1-1
Duration: since March 2016
Cooperation partner:
- Leibniz Institute for Crystal Growth (IKZ) in the Forschungsverbund Berlin e.V., Dr. Chr. Frank-Rotsch
- UMIT - Private University for Health Sciences, Medical Informatics and Technology GmbH, Prof. Dr.-Ing. Frank Woittennek
Content: A very important process for the production of monocrystalline materials is the so-called vertical gradient freeze (VGF) process. In this process, polycrystalline starting material is melted in a vertical crucible and then slowly solidified from a seed crystal at the bottom. For this purpose, a temperature field is controlled so that the melting point isotherm slowly moves upwards over the melt in the crucible. The necessary control points are realized, for example, by resistance heaters arranged around the crucible. In order to control the process, it is necessary to obtain information about the current state of the system in real time. The crystallization rate of the crystal is of particular interest. However, this cannot be measured directly. This is due to the high temperatures, the reactivity of the materials used and the purity requirements, which prohibit the placement of measuring equipment inside the crucible. Only the temperatures of the heating elements are available as measurement information. This means that it is currently impossible to directly influence the process by means of feedback (control); it is only operated as a controlled "black box". From the point of view of control theory, the process is a typical representative of the class of so-called distributed parametric systems with concentrated control action (heater) and a partially free boundary (phase boundary between melt and crystal).
The subject of the project is the theoretical and practical development of methods for establishing control of the process. This also includes methods for reconstructing the system state from the available or newly introduced measured variables. For this purpose, distribution parametric methods, which have been investigated and significantly developed at the Institute of Control Theory (TU Dresden) for many years, are to be used and further developed. The scientific knowledge gained here lies primarily in the establishment of theoretical procedures for the realization of a control system for this model class. Up to now, the focus has largely been on control and parameter identification. This is coupled with very extensive work on modeling at the Institute for Crystal Growth Berlin (IKZ). These models are required for the actual controller and observer design as well as for validating the designed control concepts in order to reduce the experimental effort. The challenge here is to set up mathematical models of the process that are sufficiently accurate, real-time capable and structurally suitable for the intended control theory methods. The methods developed are to be embedded in a theoretically demanding framework and developed strictly for practical usability and ultimately tested on the real process at the IKZ.
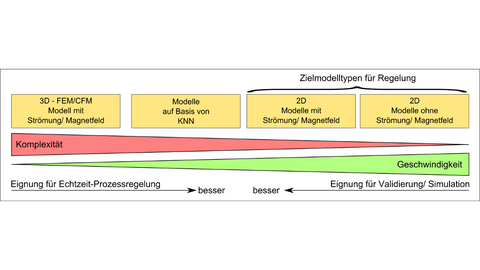
Vergleich unterschiedlicher Modelltypen und deren Eigenschaften für die Regelung.