SPP 1748: Zuverlässige Simulationstechniken in der Festkörpermechanik - Entwicklung nicht konventioneller Diskretisierungsverfahren, mechanische und mathematische Analyse

Adaptive isogeometrische Modellierung des Risswachstums in heterogenen Materialien

Bei der Entwicklung innovativer Produkte kommen neuartige aktive Leichtbaustrukturen auf der Basis von Verbundwerkstoffen mit einer ausgeprägten Mikrostruktur zum Einsatz. Die verlässliche computergestützte Auslegung dieser Komponenten erfordert die genaue, robuste und effiziente numerische Lösung nichtlinearer gekoppelter Probleme. In diesem Projekt sollen daher adaptive isogeometrische Verfahren zur dreidimensionalen Modellierung und Simulation des Deformations- und Versagensverhaltens heterogener Materialien entwickelt, implementiert und analysiert werden. Die Modellierung von Grenzflächenrissen erfolgt dabei durch die Kombination eines Kohäsivzonenmodells mit der sukzessiven Erhöhung der Knotenmultiplizitäten zur Einbringung eines Verschiebungssprungs. Für die Modellierung der Rissausbreitung innerhalb eines homogenen Materialbereiches wird dagegen ein Phasenfeldansatz genutzt, der auch Wechselwirkungsphänomene wie Rissverzweigung und -vereinigung abbilden soll. Die Isogeometrische Analyse (IGA) weist zahlreiche vielversprechende Eigenschaften neuartiger Diskretisierungsverfahren auf. Neben der exakten Abbildung geometrischer Details sind dies insbesondere eine hohe Effizienz durch die Verwendung von Ansätzen höherer Ordnung sowie die Kontrolle der Regularität der Ansatzfunktionen. Des Weiteren bietet die Nutzung von T-Splines - im Gegensatz zu klassischen NURBS - eine effiziente Möglichkeit zur lokalen adaptiven Verfeinerung des Berechnungsnetzes. Diese Adaptivität ist erforderlich, um das (quasi-)singuläre Verhalten an Materialgrenzen hinreichend genau zu approximieren und die Phasenfeldmodellierung numerisch effizient umzusetzen. Die IGA auf der Grundlage von T-Splines wurde in Benchmarks erfolgreich eingesetzt und zeichnete sich dabei durch ein robustes numerisches Verhalten aus. Dennoch fehlt bisher die mathematische Untersuchung grundlegender Verfahrenseigenschaften wie Stabilität, Konsistenz und Konvergenz im asymptotischen und präasymptotischen Bereich. Neue mathematische Strategien sind erforderlich, um diese Fragestellungen - allen voran eine praktikable Charakterisierung geeigneter T-Gitter für dreidimensionale Probleme - zu untersuchen. Die IGAFEM wird auf der Grundlage der Bézier-Extraktion, die einen einheitlichen Ansatz für die FE-Implementierung von T-Splines und NURBS bietet, realisiert. Dies erlaubt die Einbettung in eine existierende 3D FEM- und XFEM-Entwicklungsumgebung und ermöglicht die Verwendung von vorhandenen inelastischen Materialmodellen, Kohäsivzonenformulierungen und Verfahren zur Berücksichtigung großer Deformationen. Basierend auf dieser Implementierung zielt das Projekt darauf ab, Vorteile der IGA gegenüber der klassischen FEM und XFEM sowie anderen innerhalb des Schwerpunktprogrammes verfolgten Ansätzen aufzuzeigen. Zur Überprüfung und Beurteilung des neuen adaptiven isogeometrischen Berechnungsverfahrens ist in jedem Entwicklungsschritt die Lösung aussagekräftiger Benchmarkprobleme vorgesehen. Dafür sind an der Professur für Nichtlineare Festkörpermechanik folgende Aufgaben zu bearbeiten:

Entwicklung und Untersuchung adaptiver isogeometrischer Verfahren in Bezug auf Stabilität und Konvergenz
Implementierung von beschnittenen hierarchischen B-Splines (THBS) mittels Bézier Extraction
Phasenfeldmodellierung des Risswachstums in homogenen Materialien
Entwicklung von Fehlerschätzern zur Anwendung adaptiver Verfahren auf die Phasenfeldmodellierung
Diskrete Modellierung von Grenzflächenrissen mittels eines Kohäsivzonenmodelles und der sukzessiven Erhöhung der Knotenmultiplizitäten in den NURBS Geometrien
Kombination der Kontinuums- und Grenzflächenschädigung zur Modellierung des Risswachstums in heterogenen Materialien
Untersuchung und Validierung der entwickelten Modelle in gege- benen Benchmarkproblemen

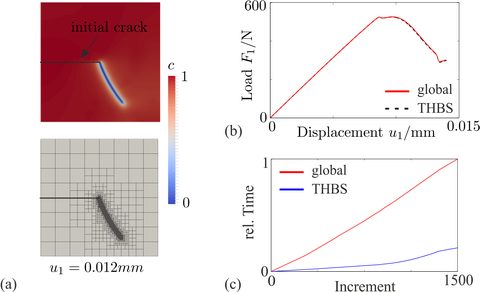
SPP1748 — Scherversuch am einseitig eingerissenen Prüfkörper: Die Anwendung der adaptiven isogeometrischen Analyse (a) auf die Phasenfeldmodellierung des Risswachstums, führt im Vergleich zu global verfeinerten Netzen zu äquivalenten Ergebnissen (b) bei reduzierten Rechenzeiten von bis zu 76% (c).

Projektmitarbeiter

Dipl.-Ing. Paul Hennig

E-Mail senden

Kontaktinformationen

Professur für Numerische und Experimentelle Festkörpermechanik

work

Besuchsadresse:

Zeunerbau, Zimmer 350 George-Bähr-Straße 3c

01069 Dresden

Zeige Karte von diesem Ort.

work Tel.
fax Fax: +49 351 463-37061

Projektleitung

Inhaber der Professur für Numerische und Experimentelle Festkörpermechanik

Prof. Dr.-Ing. habil. Markus Kästner

E-Mail senden

Kontaktinformationen

Professur für Numerische und Experimentelle Festkörpermechanik

work

Besuchsadresse:

Zeunerbau, Zimmer 352 George-Bähr-Straße 3c

01069 Dresden

Zeige Karte von diesem Ort.

work Tel.
fax Fax: +49 351 463-37061

Kooperationen

DFG Schwerpunktprogramm SPP 1748
Prof. Dr. Daniel Peterseim, Institut für Mathematik , Universität Augsburg
M.Sc. Roland Maier, Institut für Mathematik , Universität Augsburg

Publikationen

Artikel in begutachteten Zeitschriften

A. C. Hansen-Dörr, R. de Borst, P. Hennig, M. Kästner

Phase-Field Modelling of Interface Failure in Brittle Materials

submitted to Computer Methods in Applied Mechanics and Engineering
P. Hennig, M. Ambati, L. De Lorenzis, M. Kästner

Projection and Transfer Operators in Adaptive Isogeometric Analysis with Hierarchical B-Splines

Computer Methods in Applied Mechanics and Engineering, 2018. DOI
Thomas Linse, Paul Hennig, Markus Kästner, and René de Borst.
A convergence study of phase-field models for brittle fracture.
Engineering Fracture Mechanics, 2017. [ bib | DOI ]
Paul Hennig, Markus Kästner, Philipp Morgenstern, and Daniel Peterseim.
Adaptive mesh refinement strategies in isogeometric analysis— A computational comparison.
Computer Methods in Applied Mechanics and Engineering, 316, 2017. [ bib | DOI ]
M. Kästner, P. Hennig, T. Linse, V. Ulbricht
Phase-field modelling of damage and fracture – convergence and local mesh refinement
In: K. Naumenko and M. Assmus (Eds.), Advanced Methods of Continuum Mechanics for Materials and Structures, 2016. [url]
P. Hennig, S. Müller, M. Kästner
Bézier extraction and adaptive refinement of truncated hierarchical NURBS
Computer Methods in Applied Mechanics and Engineering, 2016. [url]
M. Kästner, P. Metsch, R. de Borst
Isogeometric analysis of the Cahn-Hilliard equation – a convergence study.
J. Comp. Phys. 305, S. 360-731, 2016. [url]

Konferenzbeiträge

P. Hennig, M. Kästner, M. Ambati, L. De Lorenzis
Adaptive Isogeometric Phase-Field Modeling of Ductile Fracture
7th GACM, Stuttgart, 2017
M. Kästner,P. Hennig, P. Morgenstern, D. Peterseim Bézier extraction based implementation and adaptive refinement/coarsening of truncated hierarchical NURBS 5th IGA, Pavia, Italy, 2017
M. Kästner, P. Hennig, Marreddy Ambati, Laura De Lorenzis Adaptive Phase Field Modeling of Ductile Fracture 14th COMPLAS, Barcelona, Spain, 2017
M. Kästner, T. Linse, P. Hennig, R. de Borst Gamma - convergence inphase-field models for brittle fracture
5th CFRAC, Nantes, France, 2017
P. Hennig, A. Hansen-Dörr, M. Kästner, R. de Borst
Phase-Field Modelling of Interface Failure
5th CFRAC, Nantes, France, 2017
P. Hennig, M. Kästner
Adaptive Isogeometric Phase-Field Modelling – Projection of Field and History Variables
RCM 2017, Hannover, 2017
M. Kästner, P. Hennig, P.Metsch
Adaptive Isogeometric Analysis of Phase-Field Models
ECCOMAS Congress 2016, Crete, 2016 [Abstract]
P. Hennig, M. Kästner, P. Morgenstern, D.Peterseim
Computational Comparison of Adaptive Mesh Refinement Strategies in Isogeometric Analysis
ECCOMAS Congress 2016, Crete, 2016 [Abstract]
P. Hennig, P. Metsch, M. Kästner
Efficient Phase-Field Modelling with Adaptively Refined and Coarsened Hierarchical B-splines
3^rd GAMM Workshop on Phase Field Modeling, Braunschweig, 2016 [Abstract]
P. Hennig, S. Müller, M. Kästner
Efficient Bézier extraction-based handling of adaptively refined truncated hierarchical NURBS
3^rd International Conference on Isogeometric Analysis, Trondheim, 2015 [Abstract]
M. Kästner, S. Müller and P. Metsch
Adaptive Isogeometric Phase-Field Modelling based on Hierarchical NURBS
3^rd International Conference on Isogeometric Analysis, Trondheim, 2015 [Abstract]