SPP 1748: Reliable Simulation Techniques in Solid Mechanics. Development of Non-standard Discretization Methods, Mechanical and Mathematical Analysis
Adaptive isogeometric modeling of propagating strong discontinuities in heterogeneous materials
Multi-material lightweight designs and smart devices with characteristic microscopic material structures are the key features for the development of innovative products. In this context, an adaptive isogeometric framework for the modeling and simulation of crack propagation in heterogeneous materials is to be developed, implemented, and mathematically analyzed in this project. The mechanical modeling of interface failure will be based on increasing knot multiplicities driven by cohesive zone models for crack propagation along material interfaces. In addition, a phase-field model will account for propagating cracks in the bulk material including interaction phenomena such as crack branching and coalescence. The spline-based discretization offers higher efficiency compared to Lagrangian polynomials, control of regularity, accurate approximation of strong gradients in the phase-field order parameter, as well as the possibility to discretize higher-order phase-field equations. Local mesh adaptivity required for the resolution of material interfaces and the phase-field variables will be provided by T-splines as well as hierarchical spline approximations. In addition to the physical modeling, open mathematical problems include a practicable characterization of T-meshes suitable for IGA in 3D and clear understanding of the role of increased regularity in the approximation. Consequentally, the following tasks arise:
- development and investigation of adaptive isogeometric methods concerning stability and convergence
- implementation of truncated hierarchical B-Splines (THBS) using Bézier extraction
- phase-field modelling of crack propagation in homogeneous materials
- development of error estimators for adaptive phase-field models
- modelling of interface failure based on increased knot multiplicities in spline based geometries and a cohesive zone model
- combining the crack modelling in the bulk material and the interface failure
- investigation and validation of models in benchmark problems
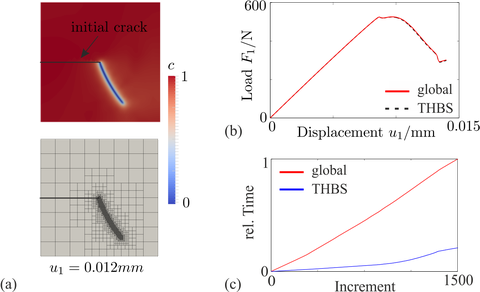
Single edge notched shear test: (a) The adaptive isogeometric method is applied to the phase-field model for brittle fracture. (b)-(c) The solution of the adaptive method is equivalent to a globally refined comparative analysis but cuts the computational time by 76%.
PROJECT STAFF
 © TUD/NEFM
© TUD/NEFM
Dipl.-Ing. Paul Hennig
Send encrypted email via the SecureMail portal (for TUD external users only).
Chair of Computational and Experimental Solid Mechanics
Visiting address:
Zeunerbau, Room 353 George-Bähr-Straße 3c
01069 Dresden
PROJECT MANAGEMENT
 © TUD/NEFM
© TUD/NEFM
Professor for Computational and Experimental Solid Mechanics
NameProf. Dr.-Ing. habil. Markus Kästner
Send encrypted email via the SecureMail portal (for TUD external users only).
Chair of Computational and Experimental Solid Mechanics
Visiting address:
Zeunerbau, Room 353 George-Bähr-Straße 3c
01069 Dresden
COORPORATIONS
DFG Schwerpunktprogramm SPP 1748
Prof. Dr. Daniel Peterseim, Institute of Mathematics , University of Augsburg
M.Sc. Roland Maier, Institute of Mathematics , University of Augsburg
PUBLICATIONS
Journals
-
A. C. Hansen-Dörr, R. de Borst, P. Hennig, M. Kästner
Phase-Field Modelling of Interface Failure in Brittle Materials
submitted to Computer Methods in Applied Mechanics and Engineering
-
P. Hennig, M. Ambati, L. De Lorenzis, M. Kästner
Projection and Transfer Operators in Adaptive Isogeometric Analysis with Hierarchical B-Splines
Computer Methods in Applied Mechanics and Engineering, 2018. DOI
-
Thomas Linse, Paul Hennig, Markus Kästner, and René de Borst.
A convergence study of phase-field models for brittle fracture.
Engineering Fracture Mechanics, 2017. [ bib | DOI ] -
Paul Hennig, Markus Kästner, Philipp Morgenstern, and Daniel Peterseim.
Adaptive mesh refinement strategies in isogeometric analysis— A computational comparison.
Computer Methods in Applied Mechanics and Engineering, 316, 2017. [ bib | DOI ] - M. Kästner, P. Hennig, T. Linse, V. Ulbricht
Phase-field modelling of damage and fracture – convergence and local mesh refinement
In: K. Naumenko and M. Assmus (Eds.), Advanced Methods of Continuum Mechanics for Materials and Structures, 2016. [url] - P. Hennig, S. Müller, M. Kästner
Bézier extraction and adaptive refinement of truncated hierarchical NURBS
Computer Methods in Applied Mechanics and Engineering, 2016. [url] - M. Kästner, P. Metsch, R. de Borst
Isogeometric analysis of the Cahn-Hilliard equation – a convergence study.
J. Comp. Phys. 305, S. 360-731, 2016. [url]
Talks
-
P. Hennig, M. Kästner, M. Ambati, L. De Lorenzis
Adaptive Isogeometric Phase-Field Modeling of Ductile Fracture
7th GACM, Stuttgart, 2017 - M. Kästner,P. Hennig, P. Morgenstern, D. Peterseim Bézier extraction based implementation and adaptive refinement/coarsening of truncated hierarchical NURBS 5th IGA, Pavia, Italy, 2017
- M. Kästner, P. Hennig, Marreddy Ambati, Laura De Lorenzis Adaptive Phase Field Modeling of Ductile Fracture 14th COMPLAS, Barcelona, Spain, 2017
- M. Kästner, T. Linse, P. Hennig, R. de Borst Gamma - convergence inphase-field models for brittle fracture
5th CFRAC, Nantes, France, 2017
-
P. Hennig, A. Hansen-Dörr, M. Kästner, R. de Borst
Phase-Field Modelling of Interface Failure
5th CFRAC, Nantes, France, 2017 - P. Hennig, M. Kästner
Adaptive Isogeometric Phase-Field Modelling – Projection of Field and History Variables
RCM 2017, Hannover, 2017 - M. Kästner, P. Hennig, P.Metsch
Adaptive Isogeometric Analysis of Phase-Field Models
ECCOMAS Congress 2016, Crete, 2016 [Abstract] - P. Hennig, M. Kästner, P. Morgenstern, D.Peterseim
Computational Comparison of Adaptive Mesh Refinement Strategies in Isogeometric Analysis
ECCOMAS Congress 2016, Crete, 2016 [Abstract] - P. Hennig, P. Metsch, M. Kästner
Efficient Phase-Field Modelling with Adaptively Refined and Coarsened Hierarchical B-splines
3rd GAMM Workshop on Phase Field Modeling, Braunschweig, 2016 [Abstract] - P. Hennig, S. Müller, M. Kästner
Efficient Bézier extraction-based handling of adaptively refined truncated hierarchical NURBS
3rd International Conference on Isogeometric Analysis, Trondheim, 2015 [Abstract] - M. Kästner, S. Müller and P. Metsch
Adaptive Isogeometric Phase-Field Modelling based on Hierarchical NURBS
3rd International Conference on Isogeometric Analysis, Trondheim, 2015 [Abstract]
