Synthese von Ratterkarten mit hochtourig drehenden Spindel-Lager-Systemen unter Berücksichtigung gyroskopischer Effekte
| Laufzeit: | 06/2007 – 05/2009 |
| Finanzierung: | DFG – SPP 1180 |
| Bearbeiter: | Dr.-Ing. Michael Löser |
Zielstellung
Zur Prognose von Stabilitätsgrenzen von Zerspanprozessen werden die Wechselwirkungen zwischen den zu einem geschlossenen Wirkungskreis verkoppelten Teilsystemen Werkzeugmaschinen-Struktur und Zerspanprozess betrachtet. Nach dem Stand der Technik sind mehrere instabilitätsverursachende Wirkmechanismen bekannt, auf die wiederum eine Vielzahl von Einflussgrößen wirken. Die Berücksichtigung dieser Mechanismen und Einflussgrößen in ihrer Gesamtheit erfolgt derzeit nur durch Simulationen im Zeitbereich. Diese Zeitbereichssimulationen sind jedoch sehr rechenzeitaufwendig. Das Ziel des Vorhabens besteht darin, Ratterkarten insbesondere unter Berücksichtigung der drehzahlabhängigen Änderung des strukturdynamischen Verhaltens von Spindel-Lager-Systemen schnell, zumindest teilanalytisch und unter Verzicht auf zeitaufwändige Simulationen im Zeitbereich zu berechnen.
Lösungsweg
Nach dem Stand der Technik sind zeiteffiziente analytische bzw. teilanalytische Berechnungsverfahren zur Analyse der Prozessstabilität bekannt, mit denen unter Berücksichtigung einzelner Effekte Ratterkarten berechnet werden. Diese Verfahren können angewandt und gegebenenfalls erweitert und/oder kombiniert werden. Damit können Sätze von Ratterkarten berechnet werden, die sich unterschiedlichen Wirkmechanismen und Einflussgrößen zuordnen lassen. Mit diesen Teilratterkarten ist die Synthese einer Gesamtratterkarte möglich. Als Referenz zur Bewertung der mit den weiterentwickelten Methoden berechneten Stabilitätsgrenzen dienen durch Simulationen im Zeitbereich ermittelte Ratterkarten.
Ergebnisse
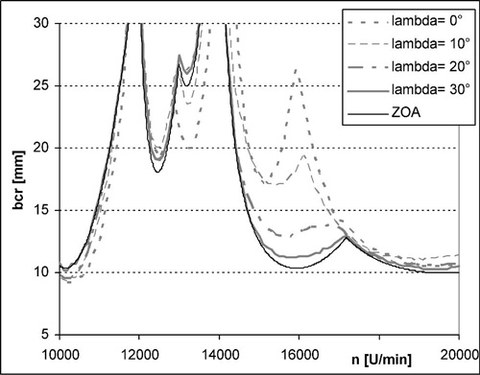
Es konnte gezeigt werden, dass für ein breites Spektrum von Prozessbedingungen die Anwendung klassischer Ortskurvenverfahren eine ausreichende Prognosegenauigkeit sichert. Diese Aussage gilt insbesondere für Prozesse bei denen gedrallte Werkzeuge zum Einsatz kommen. Diese Randbedingungen waren für den untersuchten Referenzprozess gegeben. Damit war es möglich, Stabilitätskarten unter Berücksichtigung der Drehzahlabhängigkeit des dynamischen Übertragungsverhaltens zu berechnen. Dazu wurde ein für diskrete Drehzahlbereiche konstantes Übertragungsverhalten angenommen. Für die untersuchte Referenz-Spindel erweist sich bereits eine relativ grobe Diskretisierung des Drehzahlbereiches als ausreichend. Um die Übertragbarkeit der Ergebnisse auf andere Spindel-Werkzeug-Systeme zu gewährleisten sind hierzu noch Kriterien zu erarbeiten, die eine Aussage zu der notwendigen Diskretisierung zulassen. Für Prozessbedingungen bei denen sich eine starke Zeitabhängigkeit der Richtungsfaktoren ergibt (z.B. stark unterbrochener Schnitt), können zusätzliche Rattersäcke auftreten. Dies ist Stand des Wissens. In den im Rahmen dieses Projektes durchgeführten Untersuchungen konnte gezeigt werden, dass es darüber hinaus für Systeme mit einem MDoF-Verhalten zu einer gegenseitigen Beeinflussung der Moden kommen kann. In der Praxis kann dies z.B. dazu führen, dass der Drallwinkel der eingesetzten Werkzeuge - bei ansonsten gleichen Prozessbedingungen - einen Einfluss auf die Stabilitätsgrenze besitzt. In diesem Fall ist die Anwendung klassischer Ortskurvenverfahren unter Verwendung mittlerer Richtungsfaktoren nicht mehr möglich. Ein Schwerpunkt der weiteren Arbeiten besteht daher in der Implementation eines Ortskurvenverfahren, welches die Zeitabhängigkeit der Richtungsfaktoren berücksichtigt und damit die Abbildung solcher Effekte erlaubt. Basis ist dabei die Multi-Frequency-Solution nach Altintas.
Kontakt
 © Crispin-Iven Mokry
© Crispin-Iven Mokry
Wissenschaftlicher Mitarbeiter
NameHerr Dr.-Ing. Lars Penter
Oberingenieur Forschung und Lehre
Eine verschlüsselte E-Mail über das SecureMail-Portal versenden (nur für TUD-externe Personen).
Professur für Werkzeugmaschinenentwicklung und adaptive Steuerungen
Professur für Werkzeugmaschinenentwicklung und adaptive Steuerungen
Besuchsadresse:
Kutzbach-Bau, Raum 106 Helmholtzstraße 7a
01069 Dresden